Chaosforschung heute

Es gibt viele Arten von Dynamik. Manche sind kompliziert, andere nicht. Um das besser zu verstehen, können wir ein Vektorfeld betrachten, das von nur einem Parameter abhängt, und diesen Parameter langsam ändern. Für manche Parameterwerte ist die Dynamik einfach, dann aber wird sie plötzlich kompliziert. Wie kann man diese Bifurkationen verstehen? Wie verhalten sich sich meistens?

Das sind für Mathematiker hübsche Probleme. Die Spur, die ein Attraktor in einer Ebene hinterlässt, wenn der Parameter sich ändert, sieht wie eine Borte aus. Man nennt sie Bifurkationsdiagramm. Schön, aber nicht leicht zu verstehen!

Natürlich versuchen Mathematiker in der Regel, allgemeingültige Gesetze zu zeigen. Oft aber betrachten sie zunächst nur Beispiele und hoffen heimlich, dass das, was sie am Beispiel beobachten, auch allgemein gilt.

Wie wir gesehen haben, konvergiert der Anteil der Zeit, die eine Bahn in einer Region verbringt, gegen einen Grenzwert, der nicht von der Anfangsbedingung abhängt: Das war die Idee von Lorenz (1917-2008) und der Sinaï-Ruelle-Bowen-Maße. Darf man hoffen, dass das immer der Fall ist?
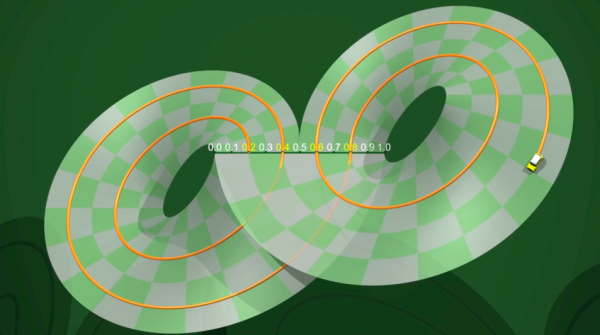
Leider nicht! Das zeigt ein kleines Beispiel von Rufus Bowen (1947-1978). Aber der Film zeigt uns, dass man dennoch diese Idee nicht zu früh aufgeben sollte, denn das Beispiel von Bowen ist sehr speziell.
In den 1990er Jahren formulierte der brasilianische Mathematiker Jacob Palis (1940-...) eine ganzen Komplex von Problemen, deren Lösungen eine globale Sicht auf das Chaos erlauben würden. Die Vermutungen von Palis sind präzise mathematische Aussagen und notwendigerweise ziemlich technisch. Sie nehmen einige Ideen aus diesem Film auf:
- Ein typisches Vektorfeld dürfte nur endlich viele Attraktoren haben.
- Eine typische Anfangsbedingung müsste sich einem dieser Attraktoren annähern.
- Jedem Attraktor müsste ein SRB-Maß zugeordnet sein, das die asymptotische Wahrscheinlichkeiten der zu ihm hinstrebenden Bahnen beschreibt.
Eine ganze Gruppe von Mathematikern arbeitet hart an diesen Vermutungen und scheint momentan Schritt für Schritt methodisch Lösungen zu finden. Aber es bleibt noch viel zu tun...

Heute stellen wir uns unter Determinismus nicht mehr die Entwicklung einer einzelnen Bahn vor, sondern denken eher an eine ganze Menge, die sich gemeinsam entwickelt. Die sensible Abhängigkeit der Bahnen von den Anfangsbedingungen wird von einer Art statistischen Stabilität der gesamten Menge kompensiert. Ist dieses Bild zu optimistisch? Die Zukunft wird es zeigen.
