Lorenz' Wassermühle
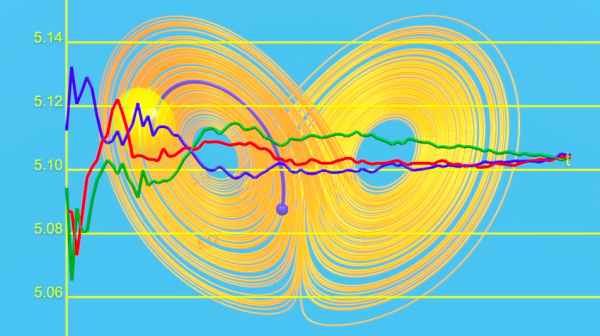
Ziel dieses vorletzten Kapitels ist es, zu zeigen, dass es einen positiven, konstruktiven Ansatz zur Lösung des Problems der Abhängigkeit von Anfangsbedingungen gibt. Das ist in der Tat die Hauptaussage von Lorenz (1917-2008), die leider einem breiten Publikum wenig bekannt ist.
« Allgemeiner behaupte ich, dass die kleinen Änderungen die Häufigkeit von Klimaereignissen wie Orkane im Laufe der Jahre weder erhöhen noch verringern. Das Einzige, was sie tatsächlich beeinflussen, ist die Abfolge, in der diese Ereignisse auftreten. »
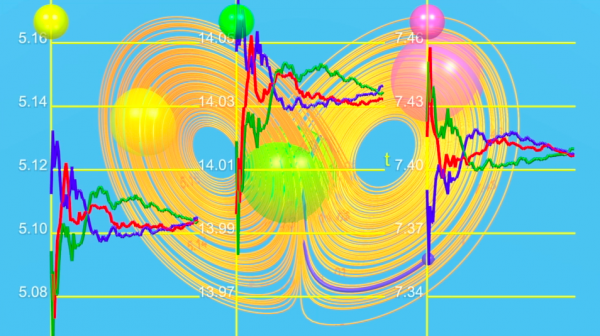
Betrachtet man drei Regionen des Raums (die z.B. Orkan-, Hitze- bzw. Schneeperioden darstellen) und misst man die Zeit, die die Trajektorien für drei zufällig gewählte Anfangsbedingungen in der jeweiligen Region verharren, so stellt man fest, dass die Zustände Orkan-Schnee-Hitze auf sich auf unverständliche Weise abwechseln und ihre Abfolge sich je nach gewählter Trajektorie unterscheidet. Aber die Zeitanteile in den Regionen konvergieren unabhängig von den Anfangsbedingungen gegen dieselben Grenzwerte. Lorenz scheint Recht zu haben!
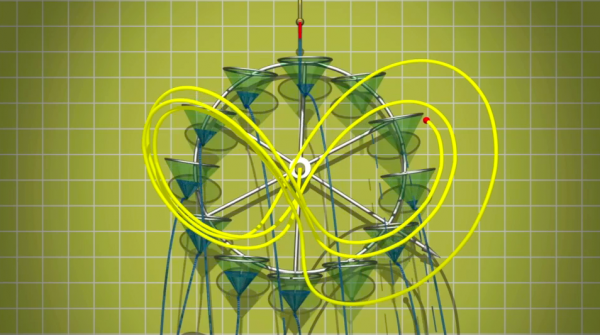
Mit Hilfe der Physiker Howard und Markus hat Lorenz ein physikalisches System entwickelt, das natürlich weit von realen Wetterphänomenen entfernt, aber dennoch schon recht konkret ist: ein Wasserrad. Drei Parameter beschreiben das Rad zu jedem gegebenen Zeitpunkt: die beiden Koordinaten seines Schwerpunkts sowie seine Winkelgeschwindigkeit. Was stellt man nun fest? Zunächst bemerkt man die Abhängigkeit von den Anfangsbedingungen. Aber die drei genannten Parameter beschreiben auch eine schöne, schmetterlingsförmige Kurve im Raum. ..
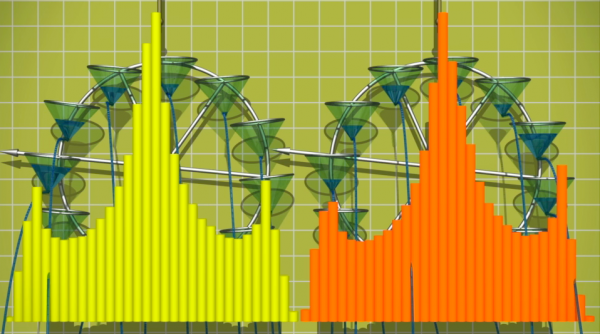
Überprüfen wir Lorenz' Intuitionen am Beispiel des Wasserrads. Wenn man zwei Wasserräder in nahezu identischen Positionen starten lässt und 25 mal pro Sekunde ihre Geschwindigkeiten misst und in ein Balkendiagramm einträgt, stellt man folgendes fest: Es scheint eine statistische Unabhängigkeit wie von Lorenz behauptet zu geben; die Balkendiagramme gleichen sich einander an.

Wenn die Zukunft einer Trajektorie statistisch nicht von den Anfangsbedingungen abhängt, sagt man, dass die Dynamik ein Sinaï-Ruelle-Bowen-Maß (SRB-Maß) besitzt. Es ist nun Aufgabe des Prognostikers, die statistische Entwicklung zu bestimmen.

Der Lorenzattraktor besitzt ein SRB-Maß. Die Temperatur entwickelt sich scheinbar zufällig... aber mit wohlbestimmten Wahrscheinlichkeiten, die es nun zu finden gilt! Durch die Einschränkung der Problemstellung auf statistische Fragen führt uns Lorenz vor, wie man das Problem des Schmetterlingseffekts umgeht und so den Anspruch der Wissenschaft, Vorhersagen treffen zu können, bewahrt. 
PDF-VERSION DES KAPITELS UND KOMMENTARE
