Das Pendel
Wie beschreibt man ein schwingendes Pendel? Die Position des Pendels kann über den Winkel zur Vertikalen bestimmt werden. Die Geschwindigkeit des Pendels ist die zweite Größe, die wir benötigen, wobei das Vorzeichen die Richtung angibt, in der das Pendel schwingt. Ohne den Luftwiederstand würde ein Pendel für immer schwingen, was Galilei (1564-1642) bereits in jungen Jahren feststellte. Dieser Wiederstand führt jedoch dazu, das ein Pendel nach einer gewissen Zeit zum Stillstand kommt.
Um ein Pendel in Bewegung zu halten, müssen wir es etwas anschieben. Reibung verlangsamt es aber mit etwas Schub zur rechten Zeit in die richtige Richtung können wir es in Bewegung halten. Wenn wir Position und Geschwindigkeit des Pendels kontinuierlich messen und in eine Grafik auftragen, erhalten wir ein sogenanntes Phasenportrait. In unserem Fall ist das eine schöne, geschlossene Kurve, die Henri Poincarré (1854-1912) einen Grenzzyklus nannte.
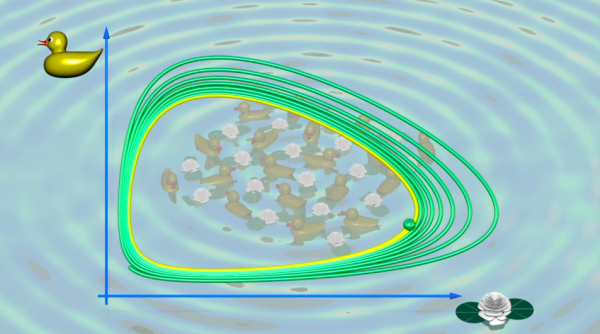
Das Lotka-Volterra Modell aus den 1930ern beschreibt einen weiteren berühmten Grenzzyklus. Es beschreibt das Zusammenspiel zweier gedachter Populationen, die sich einen Lebensraum teilen: Wasserlilien und Enten auf einem See. Zuerst gibt es wenig Enten, die sich von Wasserlilien ernähren, sodass die Anzahl der Wasserlilien zunimmt. Dadurch finden die Enten reichlich Nahrung wodurch sie sich gut vermehren und ihre Zahl zunimmt. Gibt es aber viele Enten, die Wasserlilien fressen, sinkt dien Anzahl der Wasserlilien wiederum. Durch die Nahrungsverknappung sinkt jedoch auch wieder die Zahl der Enten und der Kreislauf beginnt von vorne.
Einer der ersten Lehrsätze der Theorie dynamischer Systeme von Poincarré ende des 19ten Jahrhunderts formuliert, bestätigte die Annahme, dass solche Systeme - vielleicht nach einer Übergangsphase - schließlich in eine stabilen Zustand übergehen. Entweder durch völligen Stillstand oder durch Übergang in einen Zustand periodischer Wiederholungen. Dieser Lehrsatz gilt für Vektorfelder der Ebene.
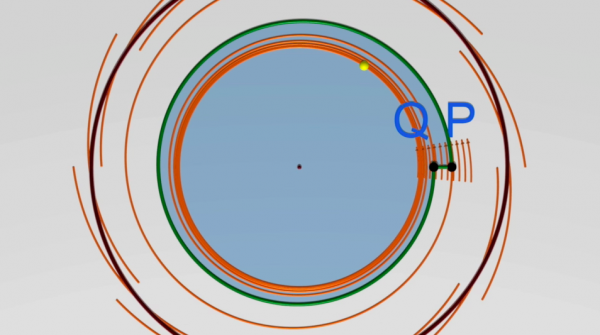
In diesem Kapitel versuchen wir, die Hauptidee dieses Satzes von Poincaré-Bendixson zu erklären. Der technische Hintergrund dieser Idee ist, dass es keine Rückkehr in einen früheren Zustand gibt: Eine Bahnkurve aus dem Punkt P kann zwar sehr nahe an P zurückkehren, jedoch niemals exakt, es sei den P liegt auf einer periodischen Bahn (dem zuvor schon erwähnten Grenzzyklus).
Dieser Lehrsatz war der Anfang der qualitativen Theorie dynamischer Systeme. Er bestätigte, dass Bahnkurven dynamischer Systeme sich irgendwann einem stabilen Gleichgewicht annähern, gilt jedoch nur für Vektorfelder der Ebene. Poincarré bemerkte bald, dass Vektorfelder des Raumes viel reichhaltigere und schönere Systeme bereithalten. Schluss mit einfachen Grenzzyklen, willkommen in der Welt des Chaos!