De schommel
Hoe kunnen we een schommelende slinger beschrijven? De positie op elk ogenblik wordt weergegeven door een getal: de hoek die de slinger maakt met een vertikale lijn. De snelheid is een tweede getal, en het teken daarvan duidt aan of de slinger naar links of naar rechts gaat. Zonder wrijving zou de slinger eeuwig blijven bewegen, en dit had Galilei (1564-1642) al vroeg begrepen. Wrijving doet echter de slinger onherroepelijk na enige tijd stoppen.
Opdat de slinger zou blijven bewegen moeten we dus duwtjes geven als de slinger vertraagt. Als we een grafiek maken met de positie en de snelheid van de slinger, dan tekenen we een fasediagram : we zien een mooie curve en Henri Poincaré (1854-1912)noemt dit een limietcyclus.
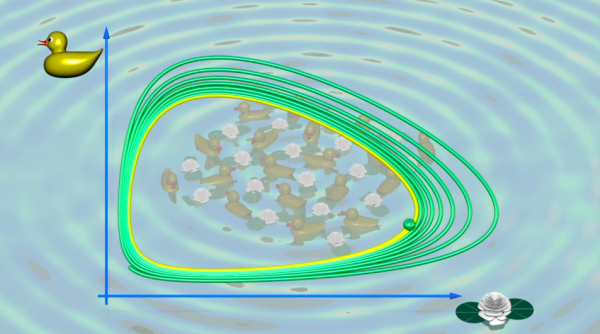
Het model van Lotka-Volterra, uit de jaren 1930, is een ander beroemd voorbeeld van een limietcyclus. Twee populaties leven in hetzelfde gebied: eenden en waterlelies. Als we ons voorstellen dat de eenden waterlelies eten, dan is het wel duidelijk dat de eenden weldoorvoed zullen zijn als er veel waterlelies zijn, en dat hun aantal zal stijgen. Maar als er dan veel eenden zijn worden er zoveel waterlelies opgegeten dat het aantal waterlelies weer daalt. De eendenpopulatie heeft niet genoeg voedsel, en wordt terug kleiner. Zo kan dan de waterlelie populatie weer aangroeien..en de cirkel is gesloten.
De overtuiging dat bewegingen zich, misschien na een korte overgangsperiode, uiteindelijk stabiliseren, door te stoppen of door
periodiek te schommelen, heeft lang de wetenschap gedomineerd. Een van de eerste stellingen in de theorie van dynamische systemen, door Poincaré in de late negentiende eeuw, leek dit te rechtvaardigen. Deze stelling gaat over vectorvelden in het vlak.
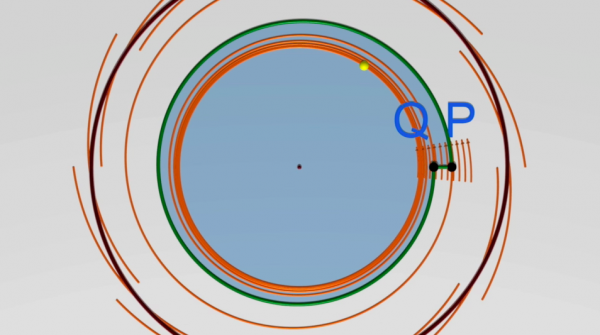
het gaat hier over de stelling van Poincaré-Bendixson. Het onderliggende idee is dat er geen recurrentie is : een baan die vertrekt vanaf een punt kan wel heel dicht terug in de buurt komen van dat punt, maar is dan veroordeeld om er ofwel telkens opnieuw terug te komen, ofwel nooit meer.
Deze stelling was het begin van de kwalitatieve theorie van dynamische systemen, maar gaat enkel over vectorvelden in een vlak. Ze zegt dus dat banen enkel periodiek kunnen worden of naar een evenwichtspunt kunnen gaan. Maar Poincaré zou al snel ontdekken dat zijn stelling alleen geldig is voor velden in twee dimensies, dat wil zeggen voor erg kleine systemen...Vanaf drie dimensies zullen we zien dat de situatie veel, veel, veel rijker ... en mooier kan zijn. Welkom in de wereld van de chaos!