O balanço
Como descrever um pêndulo que se move? A posição de um pêndulo é descrita por um número, o ângulo que ele faz com a vertical. A velocidade do pêndulo, também, é igualmente descrita por um número cujo sinal nos indica o sentido do movimento. . Sem a resistência do ar, o pêndulo se movimentaria indefinidamente, observação de Galileu ((1564-1642) já, na sua juventude. Por causa desta famosa resistência, sem nenhuma surpresa, depois de um certo tempo, o pêndulo termina por parar.
Tomemos uma situação mais realista de um balanço que é impulsionado. Como dissemos, a resistência do ar vai diminuindo o movimento. Então, é preciso impulsioná-lo novamente, a fim de acelerá-lo e de fazê-lo ir bem alto. Alguns minutos mais tarde, ele diminui a aceleração e é preciso novamente impulsioná-lo, etc. Se. a cada instante, forem medidas e registradas num gráfico a posição e a velocidade do balanço, teremos o que se chama retrato de fase; uma curva bonitinha que mostra a periodicidade do movimento, o que Henri Poincaré (1854-1912) chamou de um ciclo limite.
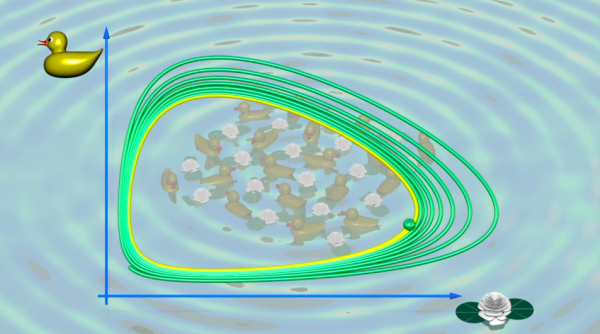
O modelo de Lotka-Volterra, nos anos de 1930, é um outro exemplo célebre que descreve duas populações compartilhando um mesmo território. Numa situação imaginária onde os patos comem nenúfares, pode-se compreender facilmente que, quando os nenúfares são muitos, os patos se alimentam bem e prosperam, e assim, o seu número aumenta. Mas quando muitos nenúfares são comidos os patos terão pouco alimento e, assim, o seu número diminue... Os nenúfares podem de novo se multiplicar e o círculo se fecha.
Um dos primeiros teoremas da teoria de sistemas dinâmicos, de Poincaré, no fim do século XIX, parece justificar a crença de que os movimentos, depois de um período de transição, podem se estabilizar, seja parando de se mover, ou oscilando periodicamente. Este teorema trata dos campos de vetores num plano.
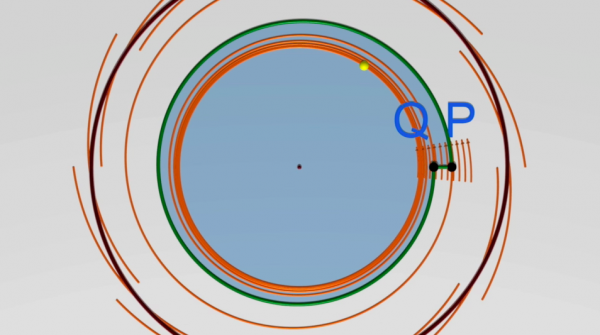
Neste capítulo tentaremos explicar a ideia principal do teorema de Poincaré-Bendixson. A ideia técnica subjacente ao teorema é que ele não pode ter uma recorrência: uma trajetória que partisse de um ponto P no plano pode num primeiro momento voltar não muito longe de P, mas, depois, ela é condenada a nunca mais voltar.
Este teorema, que marca o início da teoria qualitativa dos sistemas dinâmicos, só trata de campos de vetores no plano e confirma a ideia que as trajetórias tendem a se tornar periódicas ou se aproximar de uma posição de equilibrio. Mas Poincaré não tardaria a descobrir, que para os campos de vetores no espaço, a situação pode se tornar muito, muito mais rica e bonita. Findos os ciclos limites gentis, sejam bem-vindos ao mundo do caos!
CAPÍTULO ANTERIOR CAPÍTULO SEGUINTE
Abaixo o capítulo IV em português. Para escolher uma outra língua, acessar a lista de todos os capítulos e títulos, ou obter informações sobre a licença sob a qual este filme é difundido, ver a página O filme.