eL columpio
CAPÍTULO ANTERIOR PRÓXIMO CAPÍTULO
¿Cómo describir un péndulo que se balancea? La posición del péndulo es descrita por un número: el ángulo que forma el péndulo con la vertical. En cuanto a la velocidad del péndulo, también ésta es descrita por un número, cuyo signo nos indica el sentido del balanceo. Desde joven, Galileo (1564-1642) era consciente de que si el péndulo no tuviera fricción con el aire, se balancearía continuamente. Pero a causa del famoso rozamiento, no hay sorpresa y después de un cierto tiempo, un péndulo termina por pararse.
Interesémonos ahora por la situación más realista de un columpio que tenemos que empujar. Como hemos dicho, el rozamiento con el aire ralentiza el balanceo. Entonces, hay que empujar el columpio para acelerarlo y elevarlo muy alto. Instantes después, éste se frena de nuevo y hay que darle un nuevo impulso, etc. Si en cada instante se miden y se anotan en un gráfico la posición y la velocidad del columpio, se dibuja lo que se llama un diagrama de fase: una bonita curva muestra la periodicidad del movimiento, lo que Henri Poincaré (1854-1912) nombraba un ciclo límite.
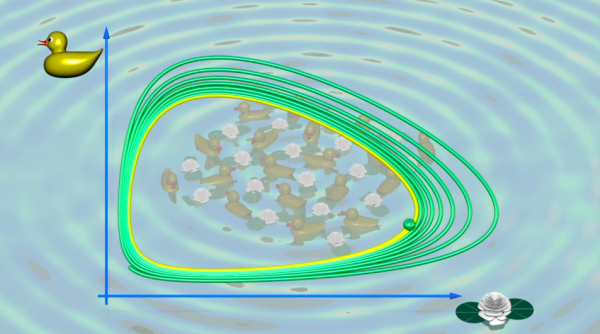
El modelo de Lotka-Volterra, que data de los años 1930, es otro ejemplo célebre que describe dos poblaciones que comparten un mismo territorio. En la situación imaginaria en la que unos patos comen nenúfares, se comprende fácilmente que mientras las plantas abunden, los patos estarán bien alimentados y prosperarán aunque su número aumente. Pero al comer muchos nenúfares, los patos terminan por encontrarse con poca comida, de manera que su población disminuye... Los nenúfares entonces pueden multiplicarse de nuevo y el círculo se cierra.
Uno de los primeros teoremas de la teoría de sistemas dinámicos, que se debe a Poincaré a finales del siglo XIX, parece justificar la creencia de que los movimientos, quizás tras un corto período de transición, terminan por estabilizarse, ya sea deteniéndose, ya sea oscilando periódicamente. Este teorema se refiere a los campos de vectores en el plano.
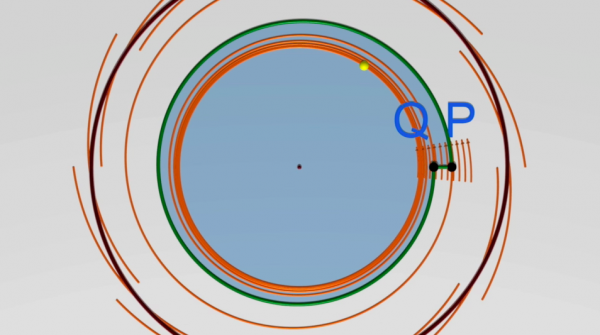
En este capítulo, se intenta explicar la idea principal de este teorema de Poincaré-Bendixson. La idea técnica que subyace es que no puede haber recurrencia: una trayectoria que partiese de un punto P del plano podría volver en un primer momento no demasiado lejos de P, pero a continuación estaría condenada a no volver jamás al punto de partida.
Este teorema, que marca el inicio de la teoría cualitativa de sistemas dinámicos, sólo vale para los campos de vectores en el plano y confirma la idea de que las trayectorias terminar por hacerse periódicas o aproximarse a una posición de equilibrio. Pero Poincaré no tardará en descubrir que, para los campos de vectores trazados en el espacio, la situación puede ser mucho más rica y bonita. ¡Se acabaron los amables ciclos límite, bienvenidos al mundo del caos!
VERSIÓN PDF DE ESTA PÁGINA Y COMENTARIOS DEL CAPÍTULO
CAPÍTULO ANTERIOR PRÓXIMO CAPÍTULO
A continuación puede verse el capítulo IV en español. Para elegir otro idioma, acceder a la lista de capítulos y subtítulos, u obtener información sobre la licencia bajo la que se difunde esta película, vea la página La película.