L'altalena
Come descrivire un pendolo che oscilla? La posizione del pendolo è descritta da un numero, l'angolo che esso crea con la verticale. Per quel che riguarda la velocità del pendolo, essa è descritta da un numero, il cui segno ci indica il senso dell'oscillazione. Senza gli attriti dell'aria, il pendolo oscillerebbe all'infinito, osservazione di cui Galileo (1564-1642) prende coscienza già nella sua più giovane età. Ma a causa di questi famigerati attriti - non ci stupiamo troppo - dopo un po', il pendolo tende a non muoversi più...
Interessiamoci allora a una situazione più realistica: un'altalena che viene spinta. Abbiamo già osservato che gli attriti dell'aria rallentano l'oscillazione. Allora bisogna spingere l'altalena per accelerarla e farla arrivare bella alta. Dopo qualche istante, essa rallenta ancora e bisogna darle una nuova spinta, etc. Se ad ogni istante misuriamo e disegnamo su un grafico la posizione e la velocità dell'altalena, ciò che disegnamo si chiama ritratto di fase: una curva simpatica testimonia la periodicità del moto, quel che Henri Poincaré (1854-1912) chiama un ciclo-limite.
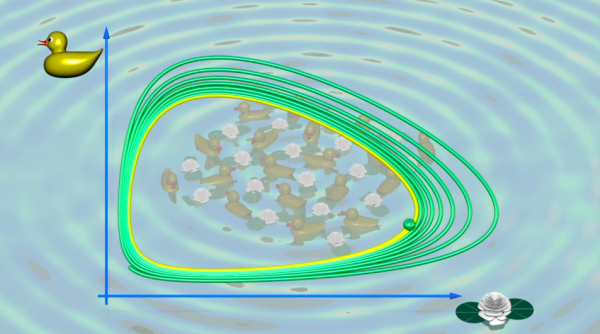
Il modello di Lotka-Volterra, che risale agli anni '30, è un altro celebre esempio che descrive due popolazioni che condividono uno stesso territorio. Nella situazione, puramente inventata, in cui delle papere mangiano delle ninfee, si capisce facilmente che, quando le ninfee sono numerose, le papere sono ben nutrite e prosperano, e così il loro numero aumenta. Ma allora molte ninfee sono mangiate e le papere si ritrovano alla fine con poco cibo e così il loro numero diminuisce... Le ninfee possono di nuovo moltiplicarsi e il ciclo ricomincia.
Uno dei primi teoremi della teoria dei sistemi dinamici, descritto da Poincaré alla fine del XIX secolo, ha parso giustificare la credenza che i moti, magari dopo un breve periodo di transizione, finiscono per stabilizzarsi, sia fermandosi, sia oscillando periodicamente. Questo teorema riguarda i campi vettoriali sul piano.
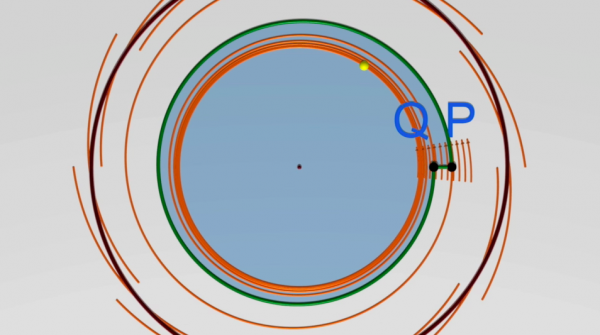
In questo capitolo, proviamo a spiegare l'idea principale di questo teorema di Poincaré-Bendixson. L’idea tecnica sottostante al teorema è che non si può avere ricorrenza: una traiettoria che parte da un punto P del piano può, in un primo tempo, tornare non troppo lontano da P, ma essa è, in seguito, condannata a mai più tornarci.
Questo teorema, che segna l'inizio della teoria qualitativa dei sistemi dinamici, riguarda esclusivamente i vettori nel piano e conferma l'idea che le traiettorie alla fine diventano periodiche o si avvicinano ad una posizione di equilibrio. Ma Poincaré non tarderà a scoprire che, per dei campi vettoriali tracciati nello spazio, la situazione può diventare molto, molto più ricca e simpatica. Fine dei cicli limite gentili, benvenuti nel mondo del caos!