单摆

我们需要两个数字来描述一个摆动的钟摆 :其一是它的位置,也就是摆线与垂线之间的夹角;其二是速度,其符号代表了它是从左到右还是从右到左。如果没有摩擦力,一个钟摆会无休无止地摆下去。伽利略·伽利莱在小时候就注意到这点了。是摩擦力使钟摆在一段时间之后停下的。


为了让一个钟摆持续摆动,我们需要推它。摩擦力使钟摆慢下来,不过如果我们在合适的时间,从合适的方向去推它,我们还是可以使它保持摆动的。我们可以将位置和速度放在图上,获得相位图。在我们的情况之中,相位图会成为一条美丽地封闭曲线。亨利·庞加莱称之为极限环。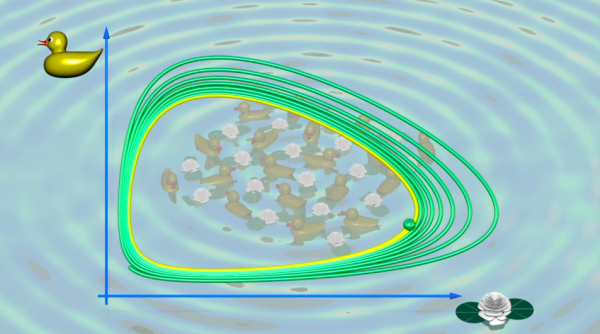
1930年代的洛特卡-沃尔泰拉模型,是另外一个有关极限环的著名例子:两个种族在同一片陆地上生存:鸭子和睡莲。假设鸭子吃睡莲,那么当有许多睡莲的时候,鸭子也会吃饱喝足,数量也会增加。不过当有太多鸭子的时候,睡莲也会被大量吃掉,睡莲的数量也减少了。鸭子的数量因为没有实物所以也减少,使得睡莲增加。因此,这个环是封闭的,然后这个过程可以循环往复。

十九世纪末期,庞加莱创立了动力系统的理论。其奠基定理之一,似乎验证了这个信念。他认为,如此的运动,可能需要经过一段过渡时期,终会以一种稳定的状态结束:抑或是所有都停止,抑或是周期性的振动。这个理论适用于平面上的向量场。
.
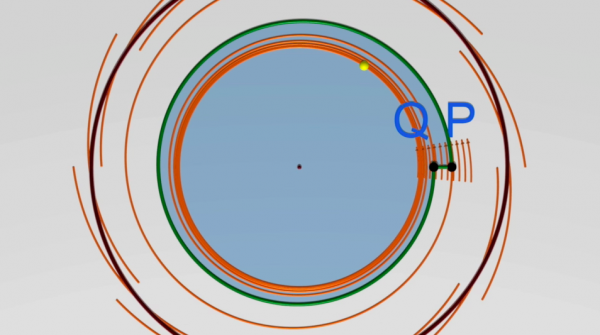
这是庞加莱-本迪克森定理。其基本思想是不存在循环:一个不经过 p 点的轨迹可以回到P点的任意小邻域,但是并不可能彻底回到 p点(除非P点是周期性轨迹上的一点)。

这个定理仅仅是动力系统理论之一,不过它只是在平面上适用。庞加莱很快就发现了,对于空间中的向量场,我们将看到很多丰富多彩且令人惊艳的现象,不再有漂亮的极限环。让我们大步踏入混沌的世界中吧。
VERSION PDF DE CETTE PAGE ET COMMENTAIRES DU CHAPITRE
CHAPITRE PRÉCÉDENT CHAPITRE SUIVANT
Ci-dessous le chapitre IV en français. Pour choisir une autre langue, avoir accès à la liste de tous les chapitres et sous-titres, ou obtenir des informations à propos de la licence sous laquelle est diffusé ce film, voir la page Le film.

