Der Schmetterlingseffekt

Im Jahr 1963 vereinfachte Edward Lorenz (1917-2008), der sich mit Problemen der Konvektion in der Erd-Atmosphäre beschäftigte, die Navier-Stokes-Gleichungen der Strömungsmechanik drastisch, die für Ihre Komplexität bekannt waren. Lorenz' vereinfachtes Modell war das, was Physiker ein "Spielzeug-Modell" nannten, da es mit den realen Bedingungen in der Atmosphäre nur noch wenig gemeinsam hatte. Lorenz stelle aber bald fest, dass dieses Modell aus mathematischer Sicht sehr interessant war. Lorenz' Gleichungen enthielten nur noch drei Parameter x, y und z, die den Zustand der Atmosphäre im (3-dimensionalen) Raum symbolisierten. Die Änderungen dieser Parameter über die Zeit folgen den Trajektorien eines 3-dimensionalen Vektor Feldes.
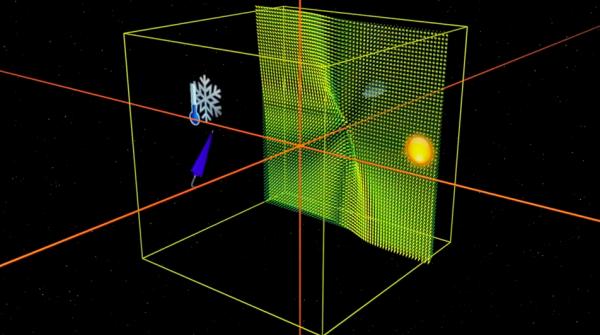

Das Verständnis der zeitlichen Entwicklung Lorenz' virtueller Atmosphäre geht auf die Verfolgung einer Bahnkurve in einem Vektorfeld zurück. Vergessen wir nicht, dass es sich um ein Spielzeug Modell handelt, dessen Ziel es ist, die Grundzüge eines sehr komplexen Systemverhaltens zu verstehen.

Si l’on considère deux atmosphères presque identiques, donc représentées par les centres de deux petites boules extrêmement proches, rapidement les deux évolutions se séparent de manière significative : les deux atmosphères deviennent complètement différentes. Lorenz a pu constater sur son modèle la dépendance sensible aux conditions initiales, le chaos.
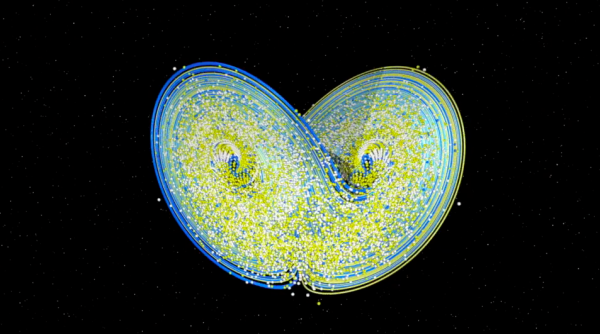
Mais plus intéressant, partant d’un grand nombre d’atmosphères virtuelles, bien qu’un peu folles et bien peu prévisibles, les trajectoires semblent toutes s’accumuler sur un même objet en forme de papillon, popularisé sous le nom d’attracteur de Lorenz, un attracteur bien étrange...
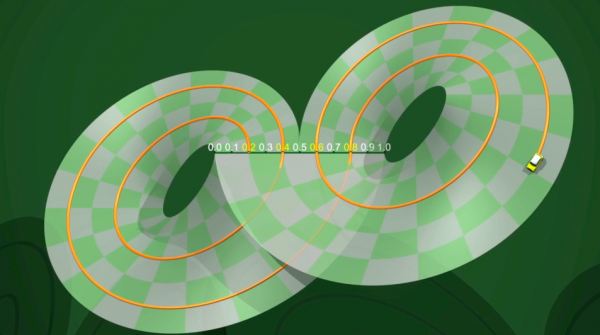
Comprendre l’attracteur de Lorenz a un véritable enjeu scientifique. À quoi ressemble-il précisément ? Comment se comporte sa dynamique interne ? C’est pour essayer de répondre à ces questions que, dans les années 1970, Birman, Guckenheimer et Williams ont proposé un modèle simple que l’on peut construire à l’aide de bandes de papier : comme pour le fer à cheval, l’on est passé d’une dynamique en temps continu à une dynamique en temps discret.
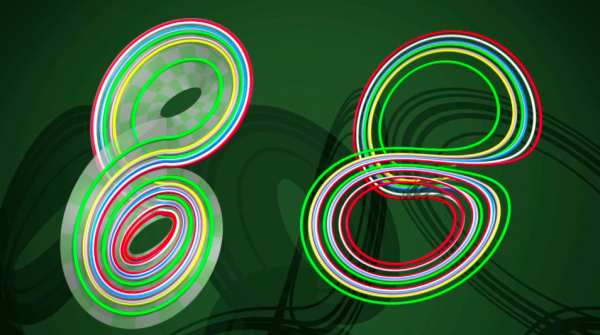
Il aura fallu attendre 2001 pour que le mathématicien Warwick Tucker démontre que les bandes de papier décrivent bien le mouvement de Lorenz : pour chaque trajectoire dans l’attracteur de Lorenz, il existe une trajectoire sur les bandes de papier qui se comporte exactement de la même manière. Même si tout ceci reste encore très simpliste par rapport au vrai phénomène météorologique, c’est une illustration du fait que les choses simples, les mathématiciens aiment !
VERSION PDF DE CETTE PAGE ET COMMENTAIRES DU CHAPITRE
Ci-dessous le chapitre VII en français. Pour choisir une autre langue, avoir accès à la liste de tous les chapitres et sous-titres, ou obtenir des informations à propos de la licence sous laquelle est diffusé ce film, voir la page Le film.
