IL MULINO DI LORENZ
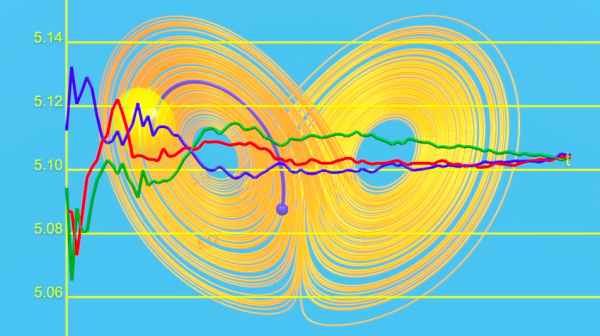
Lo scopo di questo penultimo capitolo di Caos è dimostrare che esiste un approccio positivo e costruttivo riguardo alla dipendenza sensibile alle condizioni iniziali. È il vero messaggio di Lorenz (1917-2008) che, sfortunatamente, è poco conosciuto tra il grande pubblico.
"In maniera più generale, propongo che con lo scorrere degli anni, le piccole modificazioni né aumentano, né diminuiscono la frequenza degli eventi climatici come gli uragani. La sola cosa che possono fare, è modificare l'ordine nel quale questi eventi si riproducono."
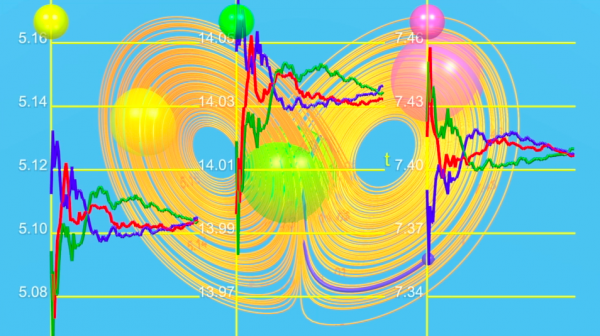
Se consideriamo tre palle nello spazio, che supponiamo rappresentare dei periodi di uragano, afa o neve, e se contiamo la proporzione di tempo passato in ogni palla per tre condizioni iniziali scelte a caso, osserviamo che le situazioni uragano-neve-afa si alternano in modo incomprensibile, diverso per ogni traiettoria. Ma le proporzioni di tempo passato nelle palle convergono verso lo stesso limite. Lorenz sembra avere ragione!
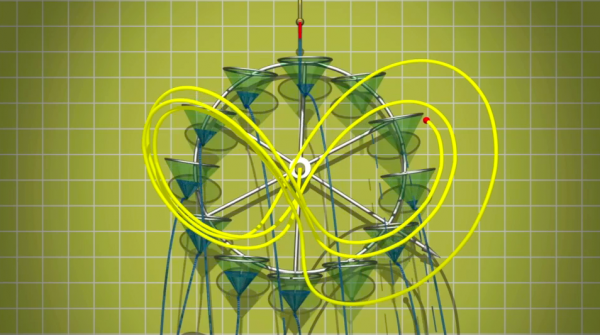
Con l'aiuto dei fisici Howard e Markus, Lorenz mise a punto un vero sistema fisico, certo ben lontano del vero fenomeno meteorologico, ma comunque concreto a tutti gli effetti: una ruota ad acqua. Tre parametri sono sufficienti per descrivere la ruota ad ogni istante: le due coordinate del centro di gravità della ruota e la velocità angolare di quest'ultima. Che constatiamo? Per prima cosa la dipendenza sensibile alle condizioni iniziali. Ma anche che i tre numeri precedenti disegnano una simpatica curva nello spazio a forma di farfalla...
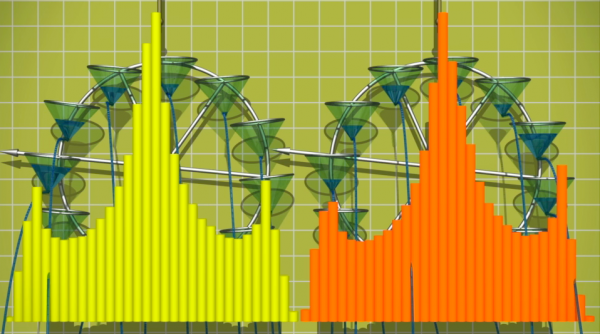
Proviamo a verificare le intuizioni di Lorenz sulla ruota ad acqua. Quando lanciamo due ruote quasi dalla stessa posizione, osservando 25 volte al secondo le loro velocità e riportando il tutto su un diagramma a colonne, cosa constatiamo? Che pare effettivamente esserci un'indipendenza statistica, come suggerito da Lorenz, i diagrammi a colonne tendono a diventare identici.

Quando la statistica del futuro di una traiettoria è insensibile alle condizioni iniziali, diciamo che la dinamica possiede una misura di Sinai-Ruelle-Bowen: una misura SRB. Lo scopo di chi fa le previsioni consiste ora nel determinare queste statistiche.

L’attrattore di Lorenz possiede una misura SRB. Tutto funziona come se la temperatura evolvesse a caso... ma con delle probabilità ben precise, che ora bisogna trovare! Collocando le proprie ambizioni attorno a dei problemi statistici, Lorenz ci mostra come evitare il problema dell'effetto farfalla e dunque preservare un carattere di predizione nella Scienza.

