L’effetTO FARFALLA

Nel 1963, Edward Lorenz (1917-2008), che si interessava al problema della convezione nell'atmosfera terrestre, semplificò drasticamente le equazioni di Navier-Stokes della meccanica dei fluidi, rinomate per la loro inestricabile complessità. Il modello atmosferico di Lorenz è ciò che i fisici chiamano modello-giocattolo: sebbene non abbia molto a che vedere con la realtà, Lorenz non tardò a rendersi conto che si trattava di un modello matematico interessantissimo. Le equazioni di Lorenz fanno intervenire giusto tre numeri x, y e z, in modo che ogni punto (x, y, z) dello spazio simbolizzi uno stato dell'atmosfera e l'evoluzione consista nel seguire un campo vettoriale.
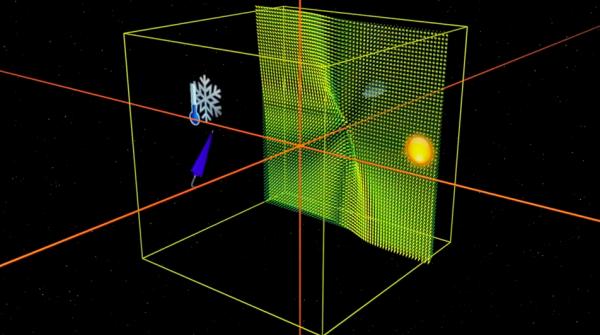

Comprendere l’evoluzione del tempo che fa nell'atmosfera virtuale di Lorenz si riduce a seguire una traiettoria di questo campo vettoriale. Non dimentichiamo che si tratta di un modello giocattolo e che l'obiettivo e tentare di capire a grandi linee un comportamento complesso.

Se consideriamo due atmosfere quasi identiche, rappresentate dunque dai centri di due piccole palle vicinissime, in brevissimo tempo le due evoluzioni di separano in modo significativo: le due atmosfere diventano completamente diverse. Lorenz ha potuto constatare sul suo modello la dipendenza sensibile alle condizioni iniziali, il caos.
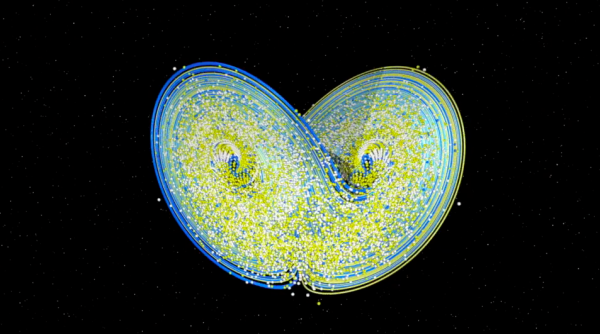
Ma la cosa più interessante è che, partendo da un grande numero di atmosfere virtuali, sebbene siano un po' pazze e ben poco prevedibili, le traiettorie sembrano accumularsi tutte su uno stesso oggetto a forma di farfalla, popolarizzato con il nome di attrattore di Lorenz, un attrattore molto strano...
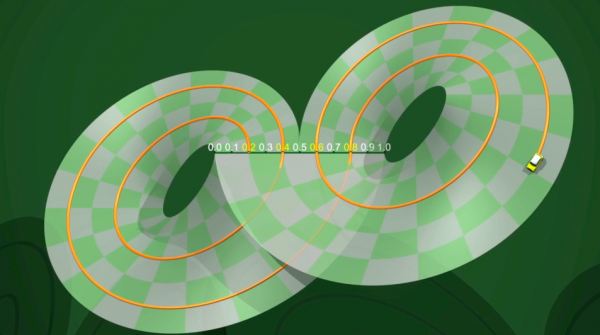
Comprendere l’attrattore di Lorenz è una vera sfida scientifica. A cosa assomiglia precisamente? Come si comporta la sua dinamica interna? Nel cercare di rispondere a queste domande, negli anni '70, Birman, Guckenheimer e Williams hanno proposto un modello semplice che si può costruire all'aiuto di nastri di carta: come per il ferro di cavallo, siamo passati da una dinamica a tempo continuo ad una dinamica a tempo discreto.
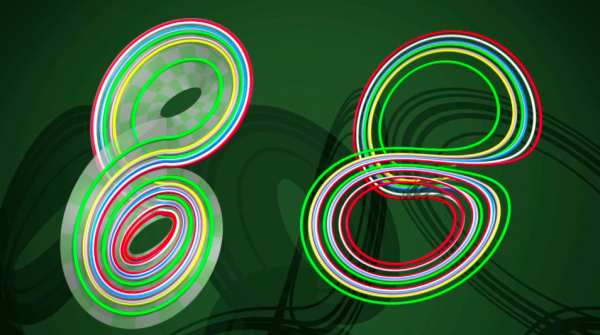
Si è dovuto aspettare fino al 2001 per la dimostrazione, fatta dal matematico Warwick Tucker, che i nastri di carta descrivono effettivamente il moto di Lorenz: per ogni traiettoria nell'attrattore di Lorenz, esiste una traiettoria sui nastri di carta che si comporta esattamente allo stesso modo. Anche se tutto ciò resta ancora molto semplicistico rispetto al vero fenomeno meteorologico, è una buona illustrazione del fatto che i matematici amano le cose semplici!
