O efeito borboleta

Em 1963, quando Edward Lorenz (1917-2008), se interessou pelo problema de convecção na atmosfera terrestre, simplificou drasticamente as equações de Navier-Stokes da mecânica dos fluidos, famosas por suas inextrincável complexidade. O modelo atmosférico de Lorenz é o que os físicos chamam de modelo de brinquedo (modelo simplificado) : mesmo que não haja grande coisa a ver com a realidade, Lorenz não demorou a concluir que se tratava de um modelo matemático muito interessante. As equações de Lorenz envolvem apenas três números x, y e z, de modo que cada ponto (x, y, z) do espaço simboliza um estado da atmosfera e a evolução consiste em seguir um campo de vetores.
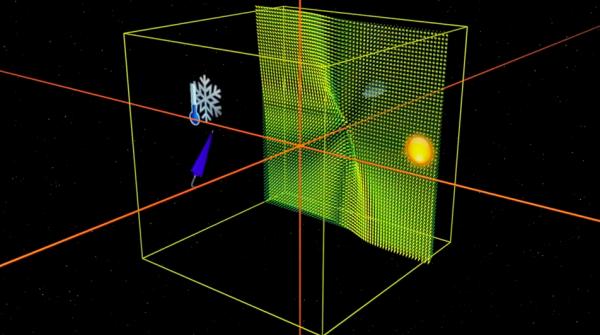

Compreender a evolução que o tempo provoca na atmosfera virtual de Lorenz consiste em seguir uma trajetória deste campo de vetores. Não nos esqueçamos que se trata de um modelo de brinquedo e que o objetivo é tentar compreender as grandes linhas de um comportamento complexo.

Se consideramos duas atmosferas quase idênticas, portanto representadas pelos centros de duas bolinhas extremamente próximas, rapidamente as duas evoluções se separam de maneira significativa: as duas atmosferas tornam-se completamente diferentes. Lorenz pôde constatar, no seu modelo, a dependência sensível das condições iniciais, o caos.
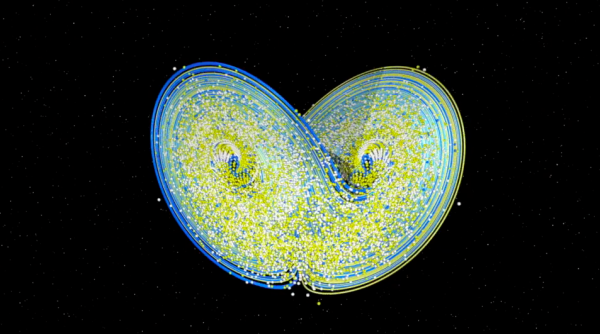
Mas o mais interessante, partindo de um grande número de ambientes virtuais, embora meio loucos e pouco previsíveis, as trajetórias parecem acumular-se num mesmo objeto em forma de uma borboleta, popularizada com o nome de atrator de Lorenz, um atrator bastante estranho...
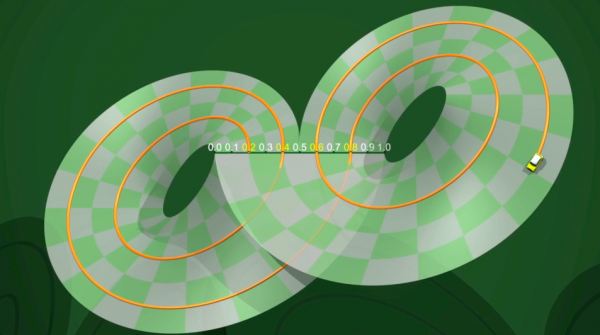
Compreender o atrator de Lorenz é um desafio verdadeiramente científico. Com o que se parece precisamente? Como se comporta sua dinâmica interna? Foi por tentar responder a estas questões que, no ano de 1970, Birman, Guckenheimer e Williams propuseram um modelo simples que se pode construir com tiras de papel: como na ferradura, passa - se de uma dinâmica em tempo contínuo para uma dinâmica em tempo discreto.
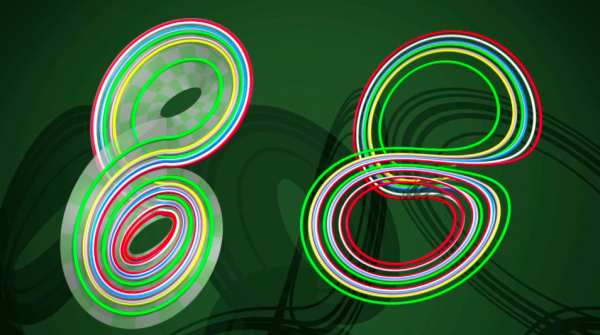
Foi necessário esperar até 2001 para que o matemático Warwick Tucker demonstrasse que as tiras de papel descrevem bem o movimento de Lorenz: para cada trajetória no atrator de Lorenz, existe uma trajetória nas tiras de papel que se comporta exatamente da mesma forma. Mesmo que tudo isto seja ainda muito simples em relação ao verdadeiro fenômeno meteorológico, é uma ilustração do fato que os matemáticos adoram as coisas simples.
CAPÍTULO ANTERIOR CAPÍTULO SEGUINTE
Abaixo o capítulo VII em português. Para escolher uma outra língua, acessar a lista de todos os capítulos e títulos, ou obter informações sobre a licença sob a qual este filme é difundido, ver a página O filme.
