El efecto Mariposa
CAPÍTULO ANTERIOR PRÓXIMO CAPÍTULO

En 1963, Edward Lorenz (1917-2008), quien se interesaba en el problema de la convección en la atmósfera terrestre, simplificó de forma drástica las ecuaciones de Navier-Stokes de la mecánica de fluidos, conocidas por su complejidad. El modelo atmosférico de Lorenz es lo que los físicos llaman un modelo de juguete: aunque probablemente no corresponda con la realidad, Lorenz no tardó mucho en darse cuenta que era un modelo matemático muy interesante. Las ecuaciones de Lorenz dependen de tres números x, y y z, de manera que cada punto del espacio (x,y,z) representa un estado de la atmósfera y para estudiar su evolución hay que seguir un campo de vectores.
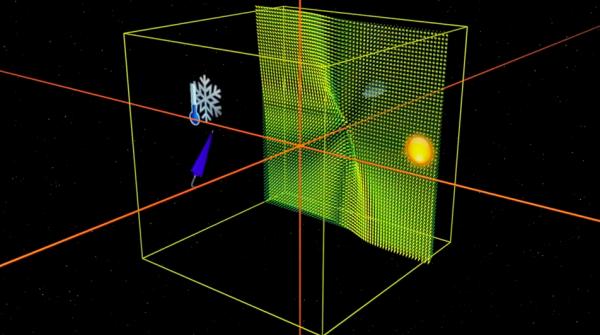

Entender la evolución del clima en la atmósfera virtual de Lorenz equivale a seguir una trayectoria de este campo de vectores. No olvidemos que se trata de un modelo de juguete y que el objetivo es tratar de entender las grandes líneas de un comportamiento complejo.

Si consideramos dos atmósferas casi idénticas, que están representadas por los centros de dos bolas pequeñas y extremadamente cercanas, en poco tiempo las dos evoluciones se separan de forma significativa: las dos atmósferas se convierten en dos atmósferas completamente diferentes. Lorenz constató en su modelo la dependencia sensible a las condiciones iniciales, el caos.
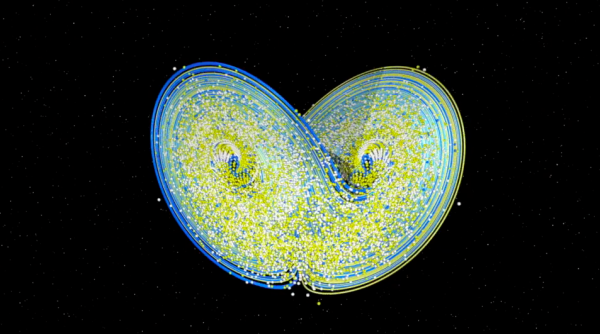
Aún más interesante: empezando con un gran número de atmósferas virtuales, aunque un poco locas y poco previsibles, parece que las trayectorias se acumulan en un sólo objeto en forma de mariposa. Conocido como el atractor de Lorenz, es un atractor bastante extraño...
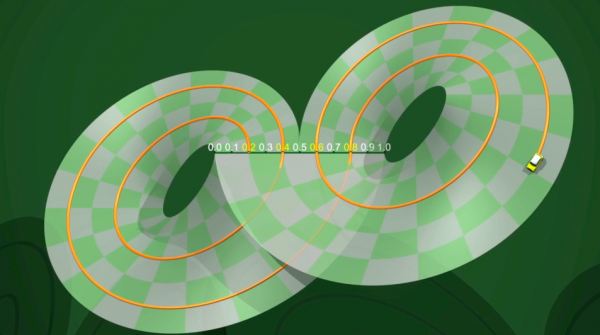
Entender el atractor de Lorenz en una verdadera cuestión científica. ¿Precisamente, a qué se asemeja? ¿Cómo se comporta su dinámica interna? Para intentar responder esta preguntas, en los años 1970, Birman, Guckenheimer y Williams propusieron un modelo sencillo que podemos construir con bandas de papel: como en el caso de la herradura, pasamos de una dinámica en tiempo continuo a una dinámica en tiempo discreto.
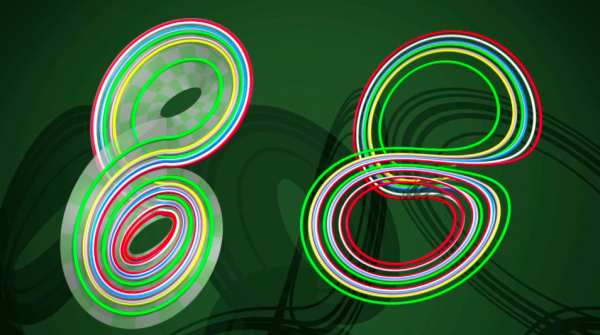
Tuvimos que esperar hasta 2001 para que el matemático Warwick Tucker mostrara que las bandas papel describen apropiadamente el movimiento de Lorenz: por cada trayectoria del atractor de Lorenz, existe una trayectoria en las bandas de papel que se comporta exactamente igual. Aunque todo esto sigue siendo un modelo simplista del verdadero fenomeno meteorológico, ilustra el hecho de que a los matemáticos les gustan las cosas sencillas.
VERSIÓN PDF DE ESTA PÁGINA Y COMENTARIOS DEL CAPÍTULO
CAPÍTULO ANTERIOR PRÓXIMO CAPÍTULO
A continuación puede verse el capítulo VII en español. Para elegir otro idioma, acceder a la lista de capítulos y subtítulos, u obtener información sobre la licencia bajo la que se difunde esta película, vea la página La película.
