バタフライ効果

1963年エドワード・ローレンツ(Edward Lorenz, 1917-2008)は,地球の大気の対流の問題に興味を持ち,解くことのできない複雑さを持つ流体力学のナビエ・ストークスの方程式を,思い切り簡単化した.ローレンツの大気モデルは物理学者がおもちゃのモデルと呼ぶものである:現実の大気との関係は恐らくほとんどないだろうが,ローレンツはこれが数学的には非常に面白いものであることに気付いた.ローレンツの方程式には,3つの実数x, y, zしか現れず,空間の各点(x,y,z)は大気の1つの状態を表し,それはベクトル場に従って変化する.
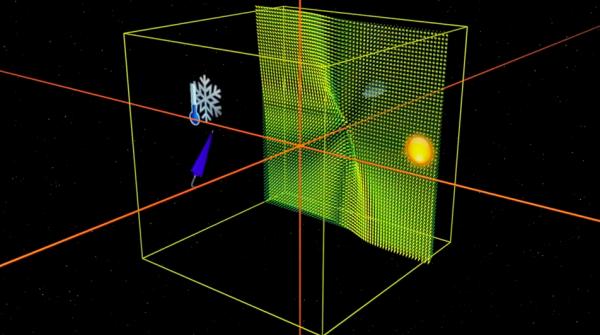

ローレンツの仮想的な大気の時間変化を理解するには,ベクトル場の軌道をたどればよい.これはおもちゃのモデルであって,複雑な挙動の大体の様子を理解することを目的に考察していることを意識して進もう.

ほとんど同じ大気の状態を考えると,それらは非常に近くにある2つの球体の中心で表されるが,時間変化とともにすぐに2つの点は遠くに離れてしまう:2つの大気の状態は全く異なるものになってしまう.ローレンツは彼のモデルが,初期条件に鋭敏に依存すること,つまりカオスを示すことを見出した.
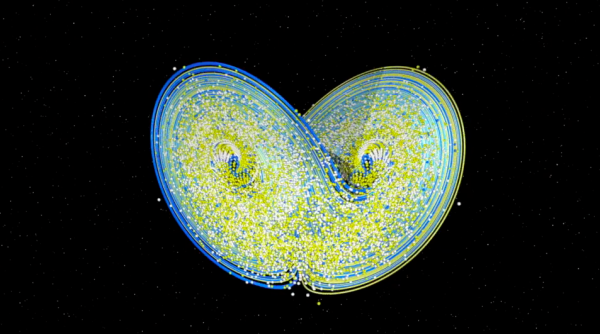
しかしもっと面白いことがある.様々な仮想的な大気状態から出発すると,少しめちゃくちゃな感じで,予測していくのは困難であるが,軌道は蝶の形をした図形に集まっていく,ローレンツ・アトラクタとして有名になった非常に奇妙なアトラクタに集まっていくのである.
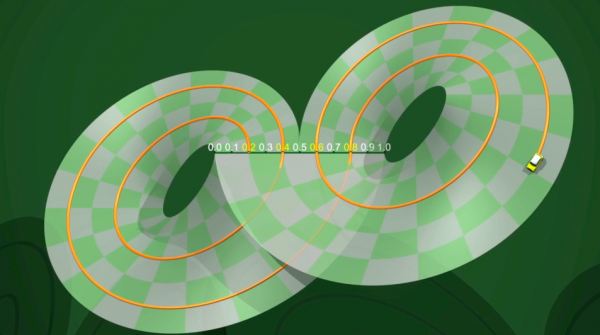
ローレンツ・アトラクタを理解することが科学者への真の問題となった.正確にはどのようなものだろうか?内部のダイナミックスはどうなっているのだろうか?この問いに答えるために,1970年代に,バーマン,グッケンハイマーとウィリアムズは,紙のテープで作ることのできる簡明なモデルを提案した:馬蹄の時と同じように,連続時刻のダイナミックスを離散時刻のダイナミックスに置き換えるのである.
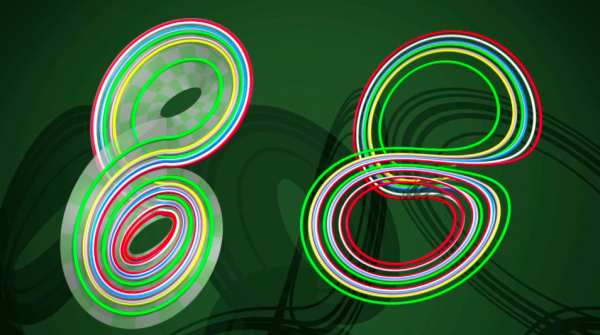
ずっと後の2001年になって数学者ワォーリック・タッカーが,紙テープのモデルがローレンツ・アトラクタにおける運動を正確に記述していることを証明した:ローレンツ・アトラクタのすべての軌道に対し,それと全く同じ運動をする軌道が紙テープのモデル上にある.これは実際の気象現象に比べて単純化されすぎているが,数学ではそういう単純なものが好まれることを表している!
以下のフランス語版の第7章をご覧ください.他の言語を選ぶ,章のリストを見る,字幕のリストを見る,このビデオを利用するためのライセンスの情報を見る,これらのためには,「このビデオについて」のページをご覧ください.
