het vlindereffect
Edward Lorenz (1917-2008), die zich interesseerde in de convectiestromen in de atmosfeer, vereenvoudigde in 1963 drastisch de vergelijkingen van Navier-Stokes, want deze laatste staan er voor bekend onoplosbaar te zijn. Het atmosferisch model van Lorenz is wat natuurkundigen een speelgoedmodel noemen: hoewel het niet veel met de werkelijkheid te maken heeft is het toch een zeer interessant model. De vergelijkingen van Lorenz hebben slechts drie variabelen x, y, z, zodat elk punt (x,y,z) van de ruimte een toestand van de atmosfeer symboliseert.
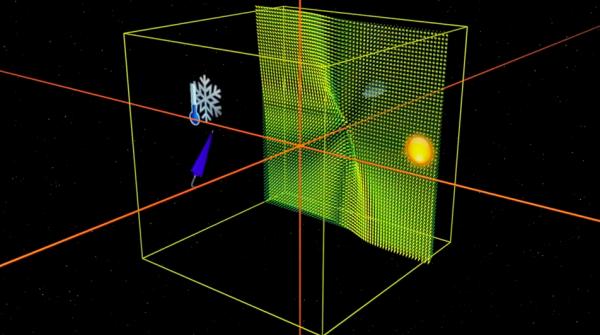

De evolutie van de atmosfeer volgen komt dan neer op het volgen van een vectorveld. Het doel van het model is om de grote lijnen van een ingewikkeld gedrag te volgen.

Als men twee toestanden van de atmosfeer neemt die zeer dicht bij elkaar liggen, dan zal de evolutie in de tijd de twee punten vrij snel uit elkaar drijven. De twee toestanden worden volledig verschillend. Die afhankelijkheid van beginvoorwaarden heeft Lorenz al waargenomen in zijn model.
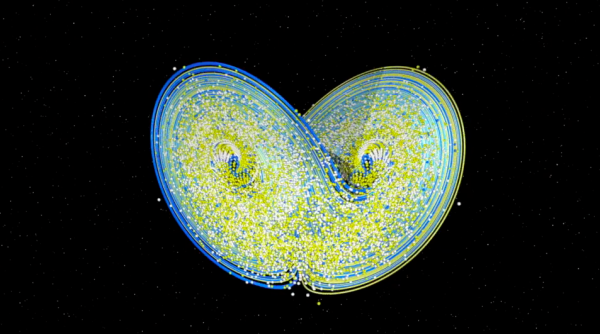
Als we vertrekken van een groot aantal virtuele toestanden van de atmosfeer evolueren alle punten naar een zelfde voorwerp in de vorm van een vlinder : de Lorenz attractor, een vreemde attractor!
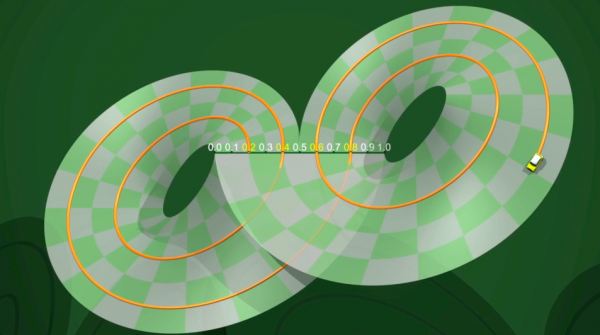
De Lorenz attractor begrijpen is een hele opgave. Wat gebeurt er juist met de interne dynamiek? In 1970 hebben Birman, Guckenheimer en Williams een eenvoudig model voorgesteld dat men simpelweg kan maken met een strook papier. Ook hier kan men de dynamiek dan bekijken in discrete tijd.
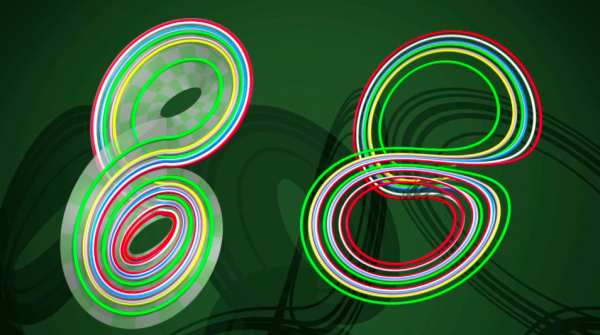
Het was slechts in 2001 dat de wiskundige Warwick Tucker bewezen heeft dat de stroken papier de bewegingen in de Lorenz attractor goed beschrijven. Voor elke baan in de attractor is er een baan op het papier die zich op exact dezelfde manier gedraagt. In vergelijking met wat er echt in de atmosfeer gebeurt is dit natuurlijk erg simplistisch, maar simpele dingen, daar houden wiskundigen van!
