L’effet papillon

En 1963, Edward Lorenz (1917-2008), qui s’intéressait au problème de la convection dans l’atmosphère terrestre, simplifia drastiquement les équations de Navier-Stokes de la mécanique des fluides, réputées pour leur inextricable complexité. Le modèle atmosphérique de Lorenz est ce que les physiciens appellent un modèle-jouet : bien qu’il n’ait probablement pas grand-chose à voir avec la réalité, Lorenz ne tarda pas à réaliser qu’il s’agissait d’un modèle mathématique très intéressant. Les équations de Lorenz ne font intervenir que trois nombres x, y et z, de sorte que chaque point (x, y, z) de l’espace symbolise un état de l’atmosphère et l’évolution consiste à suivre un champ de vecteurs.
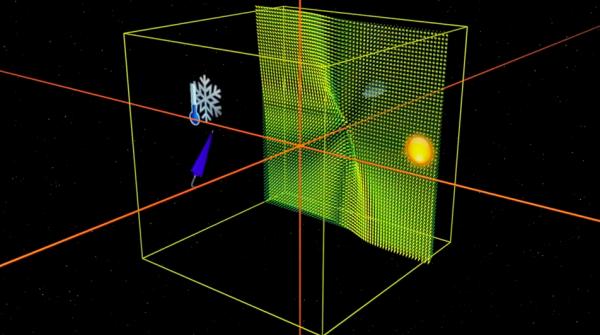

Comprendre l’évolution du temps qu’il fait dans l’atmosphère virtuelle de Lorenz revient à suivre une trajectoire de ce champ de vecteurs. N’oublions pas qu’il s’agit d’un modèle-jouet et que l’objectif est d’essayer de comprendre les grandes lignes d’un comportement complexe.

Si l’on considère deux atmosphères presque identiques, donc représentées par les centres de deux petites boules extrêmement proches, rapidement les deux évolutions se séparent de manière significative : les deux atmosphères deviennent complètement différentes. Lorenz a pu constater sur son modèle la dépendance sensible aux conditions initiales, le chaos.
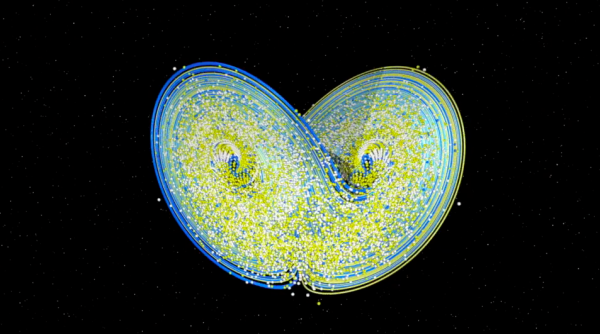
Mais plus intéressant, partant d’un grand nombre d’atmosphères virtuelles, bien qu’un peu folles et bien peu prévisibles, les trajectoires semblent toutes s’accumuler sur un même objet en forme de papillon, popularisé sous le nom d’attracteur de Lorenz, un attracteur bien étrange...
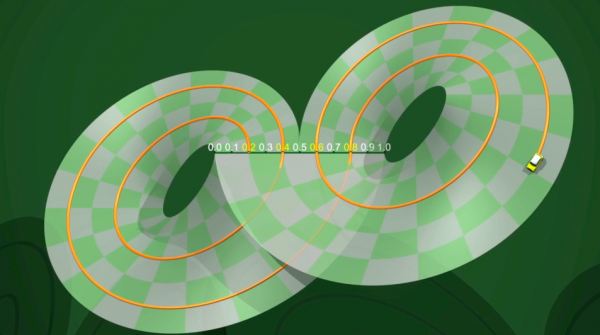
Comprendre l’attracteur de Lorenz a un véritable enjeu scientifique. À quoi ressemble-il précisément ? Comment se comporte sa dynamique interne ? C’est pour essayer de répondre à ces questions que, dans les années 1970, Birman, Guckenheimer et Williams ont proposé un modèle simple que l’on peut construire à l’aide de bandes de papier : comme pour le fer à cheval, l’on est passé d’une dynamique en temps continu à une dynamique en temps discret.
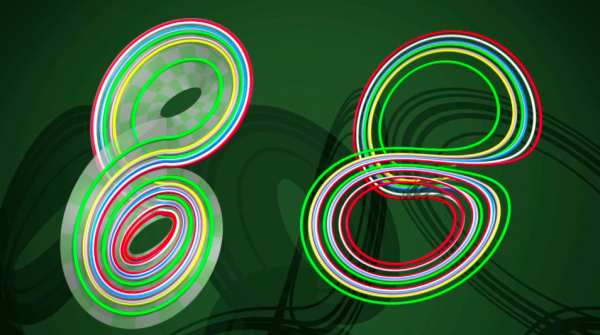
Il aura fallu attendre 2001 pour que le mathématicien Warwick Tucker démontre que les bandes de papier décrivent bien le mouvement de Lorenz : pour chaque trajectoire dans l’attracteur de Lorenz, il existe une trajectoire sur les bandes de papier qui se comporte exactement de la même manière. Même si tout ceci reste encore très simpliste par rapport au vrai phénomène météorologique, c’est une illustration du fait que les choses simples, les mathématiciens aiment !
VERSION PDF DE CETTE PAGE ET COMMENTAIRES DU CHAPITRE
CHAPITRE PRÉCÉDENT CHAPITRE SUIVANT
Ci-dessous le chapitre VII en français. Pour choisir une autre langue, avoir accès à la liste de tous les chapitres et sous-titres, ou obtenir des informations à propos de la licence sous laquelle est diffusé ce film, voir la page Le film.

Commentaires
Tout simplement fascinant!
Tout simplement fascinant! Chapeau
Tout simplement fascinant...
Tout simplement fascinant... un grand merci aux auteurs...