La balançoire

 Comment décrire un pendule qui balance ? La position d’un pendule est décrite par un nombre, l’angle que fait ce dernier avec la verticale. Quant à la vitesse du pendule, elle est également décrite par un nombre dont le signe nous indique le sens du balancement. Sans les frottements de l’air, le pendule balancerait indéfiniment, remarque dont Galilée (1564-1642) prend conscience dès son plus jeune âge. Mais à cause de ces fameux frottements, pas de surprise, après un certain temps, un pendule finit par s’immobiliser...
Comment décrire un pendule qui balance ? La position d’un pendule est décrite par un nombre, l’angle que fait ce dernier avec la verticale. Quant à la vitesse du pendule, elle est également décrite par un nombre dont le signe nous indique le sens du balancement. Sans les frottements de l’air, le pendule balancerait indéfiniment, remarque dont Galilée (1564-1642) prend conscience dès son plus jeune âge. Mais à cause de ces fameux frottements, pas de surprise, après un certain temps, un pendule finit par s’immobiliser...


Alors intéressons-nous à une situation plus réaliste d’une balançoire que l’on pousse. Comme nous l’avons dit, les frottements de l’air ralentissent le balancement. C’est alors qu’il faut pousser la balançoire afin de l’accélérer et de la faire monter bien haut. Quelques instants plus tard, elle ralentit à nouveau et il faut lui communiquer une nouvelle impulsion, etc. Si à chaque instant, sont mesurées, et reportées sur un graphique, la position et la vitesse de la balançoire, ce que l’on dessine s’appelle le portrait de phase : une jolie courbe témoigne de la périodicité du mouvement, ce qu’Henri Poincaré (1854-1912) appelle un cycle-limite.
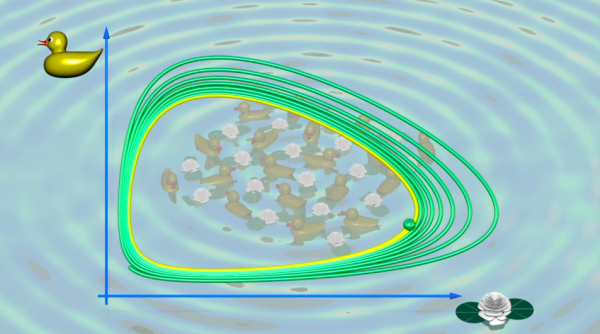
Le modèle de Lotka-Volterra, datant des années 1930, est un autre exemple célèbre qui décrit deux populations se partageant un même territoire. Dans la situation fantaisiste où des canards mangent des nénuphars, on comprend facilement que lorsque les nénuphars sont nombreux, les canards sont bien nourris et prospèrent, si bien que leur nombre augmente. Mais alors, beaucoup de nénuphars sont mangés et les canards se retrouvent finalement avec peu de nourriture, de sorte que leur nombre diminue... Les nénuphars peuvent à nouveau se multiplier et la boucle est bouclée.

L’un des premiers théorèmes de la théorie des systèmes dynamiques, par Poincaré, à la fin du XIXe siècle, a semblé justifier la croyance que les mouvements, peut-être après une courte période de transition, finissent par se stabiliser, soit en s’arrêtant, soit en oscillant périodiquement. Ce théorème concerne les champs de vecteurs dans le plan.
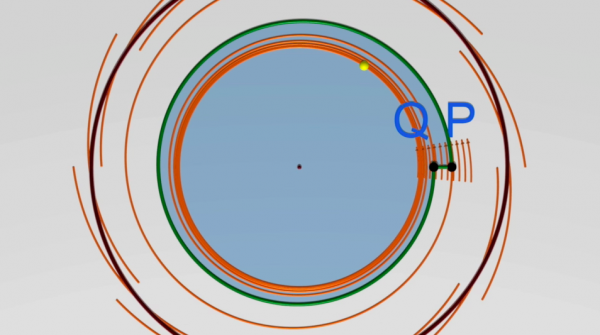
Dans ce chapitre, on essaie d’expliquer l’idée principale de ce théorème de Poincaré-Bendixson. L’idée technique sous-jacente au théorème est qu’il ne peut y avoir de récurrence : une trajectoire qui partirait d’un point P du plan peut tout à fait dans un premier temps revenir pas trop loin de P mais, ensuite, elle est condamnée à ne plus y revenir.

Ce théorème, qui marque le début de la théorie qualitative des systèmes dynamiques, ne concerne que les champs de vecteurs dans le plan et confirme l’idée que les trajectoires finissent par devenir périodiques ou s’approcher d’une position d’équilibre. Mais Poincaré ne tardera pas à découvrir que, pour des champs de vecteurs tracés dans l’espace, la situation peut devenir beaucoup, beaucoup plus riche et jolie. Finis les cycles limites gentils, bienvenue dans le monde du chaos !
VERSION PDF DE CETTE PAGE ET COMMENTAIRES DU CHAPITRE
CHAPITRE PRÉCÉDENT CHAPITRE SUIVANT
Ci-dessous le chapitre IV en français. Pour choisir une autre langue, avoir accès à la liste de tous les chapitres et sous-titres, ou obtenir des informations à propos de la licence sous laquelle est diffusé ce film, voir la page Le film.

Commentaires
That was a really nice
That was a really nice collection of beautiful pictures. It was a really nice article on Poincaré-Bendixso theorem. This theorem concerns only the vector fields in the plane and confirms the idea that the trajectories eventually become periodic or approaching an equilibrium position.
Extraordinaire !
Extraordinaire !
Moi qui vais allé l'année prochaine en FAC de mathématique,
Ce travail me permet de découvrir les mathématiques et d'éclaircir certaines choses dans mon esprit.
Super travail !
Merci à Jos Leys, Etienne ghys, Aurélien Alvarez et à toute l'équipe.
- je me presse de regarder la suite -
Bonjour,
Bonjour,
Quelque chose me gêne dans l'esquisse de preuve du théorème de Poincaré-Bendixon :
"Si la trajectoire se croise, cela contredit le théorème de Cauchy-Lipschitz, qui dit qu'un point n'a qu'une seule trajectoire." Ici, chaque point de la courbe a bien toujours une seule trajectoire, non ? Je ne vois pas la contradiction.
Ne peut-on pas plutôt dire simplement que si la trajectoire se croise, alors elle est revenue à un point antérieur et donc reproduira ce cycle pour toujours [CQFD] ?
Merci de tout cœur pour cette merveilleuse série de vidéos !
Perdu dans un champ de
Perdu dans un champ de vecteurs ...
Au ch.3 nous avons vu que les vecteurs se représentent par des flèches ; le champ de vecteurs était comme un champ de blé, chaque vecteur étant une tige de blé plantée en un point du champ. (Dommage que, pour l'exemple choisi, il fallait supposer que le blé était abattu ...)
Au ch.4, vous nous proposez d'étudier comment varient ensemble deux paramètres du pendule : sa position, qui est un point dont la trajectoire est un arc de cercle et sa vitesse où nous reconnaissons le vecteur que vous aviez présenté attaché au lego. L'enregistreur cylindrique trace le graphe du mouvement du pendule amorti par les frottements, puis un graphe différent quand le mouvement est entretenu.
Voilà maintenant que vous considérez ce graphe comme un champ de vecteurs. Pour celui qui a suivi et bien assimilé les cours de maths du secondaire, le rétablissement est facile, on l'a habitué à considérer qu'on n'a pas besoin d'une flèche pour représenter un vecteur, il suffit que son extrémité soit rapportée à un repère qui lui assigne des coordonnées : il devine donc qu'on ne parle plus du vecteur vitesse qu'on vient de nous montrer, mais du vecteur (x;v). Autre rétablissement, un peu plus facile : la trajectoire dont vous parlez maintenant n'est pas celle du pendule sous son point d'accrochage mais celle de ce vecteur dans son système d'axes.
Quant à la périodicité du mouvement étudié, je ne vois pas comment le portrait de phase la montre, puisque ce graphe ne connaît pas le paramètre temps.
Remarque marginale : on m'avait dit que c'est justement la périodicité qui intéressait Galilée ; sa chance est d'avoir pu en juger parce qu'il devait aller tous les dimanches sous le plus lent pendule d'Europe, le lustre accroché sous la coupole de la cathédrale de Pise. Son pouls lui donnait une mesure valable de la durée des oscillations.
Bonjour,
Bonjour,
Je ne suis pas certains d'avoir saisi votre première question mais je tente d'y répondre malgré tout:
La figure qui suit permet de voir le champ de vecteur et la trajectoire à la fois.
http://commons.wikimedia.org/wiki/File:Van_der_pols_equation_phase_portr...
La "trajectoire" du pendule présentée dans la vidéo ne représente plus les positions successives du pendule (comme dans le cas des legos), mais les positions successives sur l'axe X (horizontal) et leur vitesses correspondantes sur l'axe Y (vertical). La trajectoire est alors le graphe des états (position, vitesse) successifs. C'est un moyen très pratique en physique pour représenter tous les états d'un système sur un même graphe. On se débarrasse du temps mais en échange on peut en déduire plein de choses.
Pour la périodicité: si on suppose que cette trajectoire est continue et que le système ne s'arrête pas sous l'effet des frottements alors on peut en conclure une périodicité du mouvement.
Le pendule ne s'arrête jamais et passe par tous les points successifs du graphe (ici, les points sont si nombreux qu'ils forment une ligne continue), chaque point représente une position et une vitesse. Cet état du système force le pendule se mettre dans son état suivant, représenté par le point suivant du graphe. Le pendule va donc passer successivement par tous les points du graphe.
Maintenant, en supposant que le graphe soit une courbe fermée comme dans ce cas, le pendule va nécessairement retourner vers un état qu'il a déjà connu! Et cet état va forcer le pendule à se mettre dans son état suivant, à nouveau. Le pendule va donc, lors de son nouveau cycle se comporter comme lors du premier.
On en déduit donc, que si la courbe est fermée, non-seulement le mouvement est infini, mais aussi périodique. Le mouvement du pendule est entièrement déterminé et se répète identiquement.
Belles animation mais il
Belles animation mais il manque un fil conducteur entre les différents concepts expliqués (contexte historique, chronologique,physique...) et leur application.
Et puis pourquoi avoir pris des canards et des nénuphars. Tout le monde sait qu'un canard ca ne mange pas de nénuphars ... pourquoi ne pas avoir laissé les animaux d'origine : renard et lemmings ! (difficile a faire en pov?)