Смейл в Копакабане

Предыдущая глава Следующая глава

Начнём со старой идеи Анри Пуанкаре (1854-1912): изучая векторное поле в пространстве, иногда мы можем найти маленький диск, который траектории время от времени пересекают. Изучать точки на диске, в которых траектории его пересекают, зачастую много проще, чем изучать векторное поле в целом. Мы переходим от динамики с непрерывным временем к динамике с дискретным временем.

В начале 1960х, молодой американский математик Стивен Смейл (1930-...) работал на пляже в Копакабане, когда он совершил открытие... Он открыл подкову! Не настоящую, разумеется, а математический объект: преобразование, совмещающее в себе растяжение, сжатие и сгибание. Оно преобразует квадрат в подкову.

Динамика подковы очень богата, как в будущем, так и в прошлом, со структурой, бесконечно повторяющей себя. Фильм показывает подкову «под микроскопом», чтобы лучше понять её сложность.

Как понять динамику такого объекта? Идея состоит в том, чтобы поступить так же, как и для бильярда — обозначить через  A и B две вертикальные полосы. Удивительная вещь состоит в том, что мы получаем почти такие же результаты, как и Адамар для своих геодезических и для бильярда. А именно, для каждой последовательности букв A и B, даже с повторениями, — например, для BABB, — найдётся периодическая точка, путешествующая именно таким образом. Более того, такое же утверждение — что найдётся точка, итерации которой именно в данной последовательности посещают полосы — верно и для бесконечных последовательностей ! Невероятно, не правда ли ? Всё возможно... неплохой слоган для хаоса!

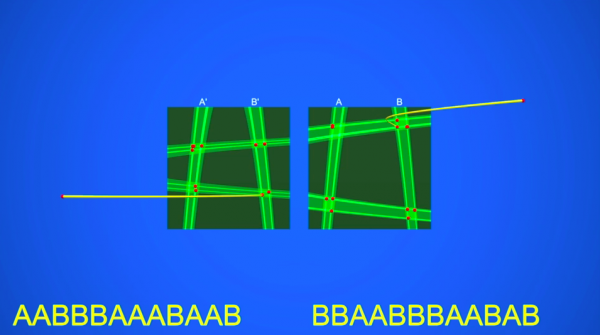
Но всё ещё интереснее! Смейл доказывает, что подкова устойчива. Небольшая её деформация не разрушает богатство динамики её траекторий: чувствительность траекторий к начальным условиям оказывается неуничтожимой. Более того, траектории двух близких подков устроены одинаковым образом — в фильме для иллюстрации показаны рядом две разные подковы с соответствующими траекториями.  Математики называют это структурной устойчивостью.

Одновременное присутствие хаоса, и потому неустойчивости отдельных траекторий, и структурной устойчивости, глобального свойства динамики, — совершенно замечательны!

Предыдущая глава Следующая глава