斯梅尔在科帕卡巴纳

首先,让我们先说一个亨利庞加莱(1854-1912)的原始想法:当我们研究空间中的向量场时,我们有时可以找到一个小的圆盘,使轨迹反复地击打在圆盘上。研究这小圆盘上的点通常比研究整个向量场好容易得多。这样我们就把连续变化的向量场上的动力系统替换成为随离散时间变化的动力系统。

二十世纪六十年代初,年轻的美国数学家史蒂芬斯梅尔在科帕卡巴纳海滩上思考时,得到了一个新发现。他发现了一个马蹄铁。当然,不是在沙滩上!事实上他的马蹄铁,是一个抽象的数学概念:一种融合了压缩和缩放的变换,当然也是一种折叠。他将一个正方形转换成了马蹄形。

这马蹄铁的动力系统是非常丰富多彩的而且对于未来和过去都是永久连续的。本章影片着重讲述了此马蹄铁是如何反复不断地复制变化的。

为了更好地理解它的动力系统,我们把两条垂直的条带称为A和B。令人惊奇的是我们得到了和阿达玛的台球测地线几乎相同的结果。对于每一个由A和B组成的有限序列,甚至包括那些可重复的,都有一个周期点恰好遵循这条路线。没有什么是不可能的!作为混沌的口号再好不过了!
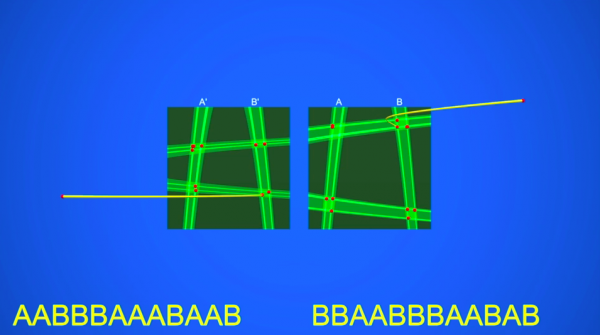

更好地;斯梅尔证明了马蹄铁是稳定的。我们可以分解他,但是其内部的动力系统还是相同的:其轨迹依旧对初始条件很敏感。数学家将这个称之为结构稳定性

混沌性,既有单个轨迹的不稳定性,又有结构稳定性,一个整体性质,并且这两者并存。这绝对是一个令人瞩目的现象。
VERSION PDF DE CETTE PAGE ET COMMENTAIRES DU CHAPITRE
CHAPITRE PRÉCÉDENT CHAPITRE SUIVANT
Ci-dessous le chapitre VI en français. Pour choisir une autre langue, avoir accès à la liste de tous les chapitres et sous-titres, ou obtenir des informations à propos de la licence sous laquelle est diffusé ce film, voir la page Le film.
