ثـــــــــــور دوهــــــــــام

عندما نتطرق إلى مسألة معقدة كالمسألة المتعلقة بحركة الأجسام السماوية ليس من غير المعقول أن نبدأ بدراسة وضعيات أكثر بساطة. إذا كانت حركة كرة تتدحرح داخل إناء لا تبدو عصية على الفهم فإن الأمر مختلف تماما بالنسبة إلى إناء يشمل نتوءات... تصبح الحركة فجأة معقدة جدا.

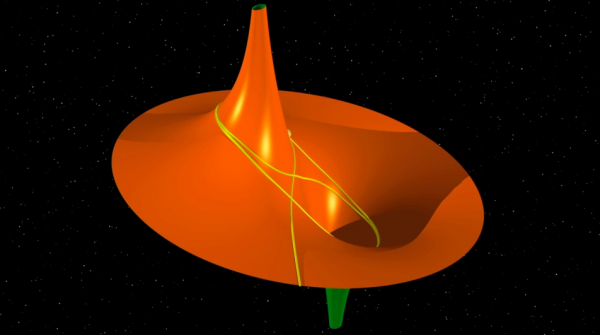
في مطلع القرن العشرين كان فيلسوف العلوم پيير دوهام (1861-1916) يستمتع بعرض أعمال الرياضياتي جاك هادامار (1865-1963) المنشورة سنة 1898 في مقالة عنوانها "حول جيوديزيات السطوح ذات انحناءات متناظرة،" بشكل خيالي: يتعلق الأمر برمي كرة على جبهة ثور تم تمديد قرنيه إلى مالا نهاية. ما أغربها من فكرة.
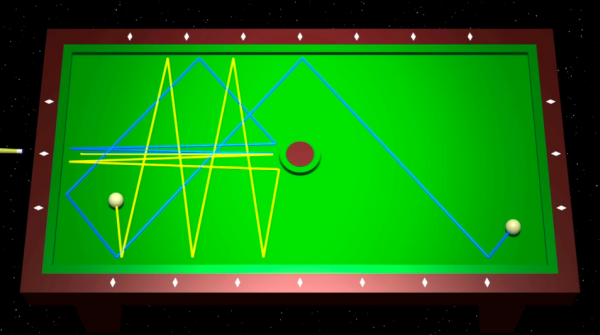
في هذا الفصل نحاول تفسير أفكار هادامار عبر مثال مختلف، لكنه قريب بما يكفي من الجيوديزيات على سطوح ذات انحناءات متناظرة : يتعلق الأمر بلعبة البليار. ماذا نلاحظ إذا وضعنا قطعا مستديرة في وسط طاولة بليار؟ نلاحظ أن كرتين مرميتين في اتجاهين متقاربين جدا، يمكن أن يكون لهما مساران مختلفان تماما.

لكن هناك أفضل من ذلك. إذا وضعنا ثلاث قطع مستديرة ا، ب، ج على الطاولة فإنه من أجل كل كلمة مكونة من هذه الحروف الثلاثة، ا ب ا ب ج ا ب ج على سبيل المثال، يوجد مسار دوري وحيد يمر على التوالي بهذه القطع الثلاث، وفق الترتيب الذي عليه هذه الحروف. ترميز المسارات هذا بكلمات متكونة من الحروف ا ب ج يذكرنا بكتابة الأعداد الحقيقية ...
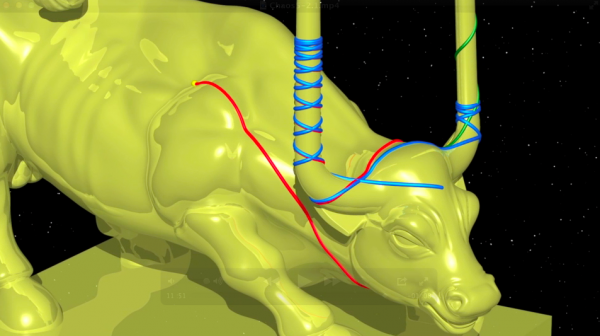
يواصل دوهام وصفه المتخيل لكتلة مادية تنزلق على جبهة ثور بهذه الكلمات.
" هناك أولا جيوديزيات تنغلق على نفسها. وهناك أخرى دون أن تمر تماما من جديد على نقطة بدايتها، لا تبتعد عنها أبدا بشكل غير منته؛ البعض يدور دونما انقطاع حول القرن الأيمن فيما يدور الآخر حول القرن الأيسر [ ... ] وهناك أخرى أكثر تعقيدا تتناوب دوراتها التي ترسمها حول أحد القرنين ، وفق قواعد محددة، مع تلك التي ترسمها حول القرن الآخر على جبهة ثورنا [ ... ]، ستوجد جيوديزيات تذهب إلى ما لا نهاية، بعضها يتسلق القرن الأيمن، والبعض الآخر يتسلق القرن الأيسر، [ ... ] " [ ... ]

جيوديزيتان تنطلقان في اتجاهين متقاربين جدا لهما مستقبلان مختلفان جدا، كما يصف دوهام ذلك بطريقة جميلة جدا.
" إذا رُميت نقطة مادية على السطح الذي تتناوله الدراسة، من موضع معطى هندسيا، وبسرعة معطاة هندسيا، فإن الاستنتاج الرياضياتي يستطيع تحديد مسار هذه النقطة وتحديد ما إذا كان هذا المسار سيبتعد إلى ما لا نهاية أم لا. لكن بالنسبة إلى عالم الفيزياء فلن يكون هذا الاستنتاج قابلا للاستعمال أبدا."
لاحظوا الاستقرار : الاستنتاج الرياضياتي ممكن بينما هو غير قابل للاستعمال بالنسبة إلى الفيزيائي. بين النظرية والتطبيق يوجد عالم بكامله.
النسخة بي دي إف لهذه الصفحة وتعليقات الفصل
ها هو أسفله الفصل 5 من الفيلم بالعربية. لاختيار لغة أخرى، للوصول إلى قائمة كل الفصول والترجمات التحتية، أو للحصول على معلومات بشأن الترخيص الذي يتم تحته نشر هذا الفيلم، انظروا الصفحة الفيلم.
