迪昂的公牛

研究天体的运动是非常复杂的,所以让我们来看一个更加简单的例子。一个在碗中的球的运动是看起来应该不是很难来理解。不过如果在碗里有一些凸起,那么这球的运动就变得非常复杂了。

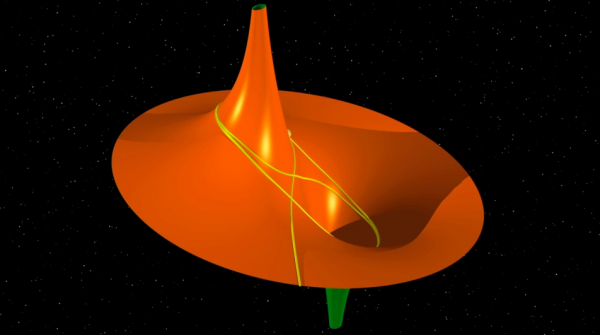
在二十世纪之初,科学哲学家皮埃尔迪昂(1861-1916),介绍了数学家杰克阿达玛(1865-1963)在1898年以如下标题发表的内容:相反曲率曲面上的测地线。迪昂说的是一个物体从一个无限长的牛角上忽略摩擦力地落下。一个奇怪的想法,不是么?
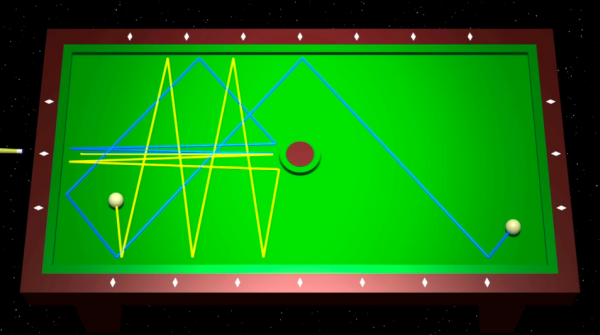
我们先试着用一个简单的例子来解释阿达玛的想法:有桌球和一个圆柱形的障碍物,两个桌球撞击这个障碍物可以在很快的时间内走出完全不同的轨迹,即使他们的起始方向十分相似。

现在我们有一张无阻力的桌子和桌子上的三个圆柱形障碍物,A,B和C,它们以圆柱形排列。这三个字母的每一种排列组合,例如,ABABCABC……,总存在一种轨迹使这个桌球以字母排列顺序在其对应的障碍物之间弹。(当然AA是不可能的)。
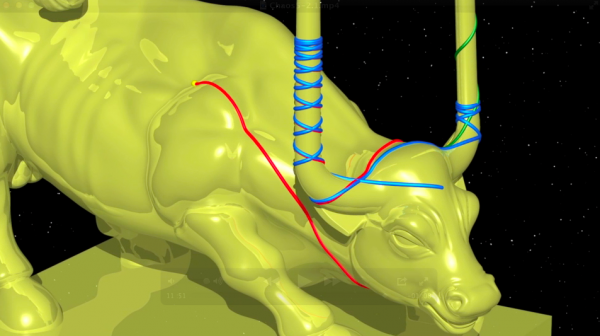
这是迪昂关于物体从牛角上滑下的描述的一部分:
首先,有封闭的测地线。还有其他的测地线,虽然不会正好回到原本的出发点,但也不是无限距离;有些测地线总是围绕右边的牛角,另外一些则围绕左边;还有的更复杂,根据某种规则,在两角之间穿梭:在一只牛角上绕完预设的圈数后,又转到另一只角上绕预设的圈数。在这个牛的头颅上,还有趋于无尽的测地线:有的沿着右边牛角盘旋上升,有的则沿着左边的慢慢远离。

两条以相似方向出发的测地线可以走出完全不同的路线,迪昂是这样形容的:
.
如果在一个表面上滑出一个质点,并在几何上精确地给定它的初始位置和速度,那么通过数学推导,便可以确定这点的轨迹,并可以断言这轨迹是否会趋于无穷。不过对于物理学家而言,这种推论是毫无用处的。
注意这点巧妙的描述:测地线可以被数学方法计算,但是对于物理学却毫无用处。
这就是理论和实际的区别!
VERSION PDF DE CETTE PAGE ET COMMENTAIRES DU CHAPITRE
CHAPITRE PRÉCÉDENT CHAPITRE SUIVANT
Ci-dessous le chapitre V en français. Pour choisir une autre langue, avoir accès à la liste de tous les chapitres et sous-titres, ou obtenir des informations à propos de la licence sous laquelle est diffusé ce film, voir la page Le film.
