デュエムの雄牛

天体の運動のように複雑な問題に取り組むために,もっとずっと簡単な状況の研究から始めるのは,十分理由のあることである.ボールの上で摩擦がない状態で玉を転がすことの理解が難しくないとしても,少し凹んだボールの上では,まったく状況は異なる…運動は突然,非常に複雑になるのである.

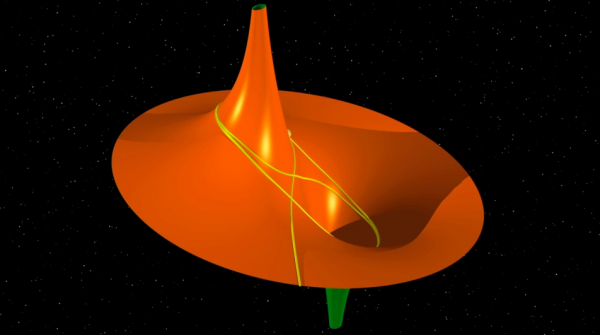
20世紀の初め,科学哲学者ピエール・デュエム(Pierre Duhem, 1861-1916) が,数学者アダマール(Jacques Hadamard, 1865-1963) の「逆の曲率を持つ曲面上の測地線について(Sur les géodésiques des surfaces à courbures opposées)」という1898年に出版された論文に書かれている仕事を,まさに比喩的に紹介しようとしている:摩擦なく転がる玉を無限に長い角をもった雄牛の額の上で転がすのだ.おかしな考え方ではないか!
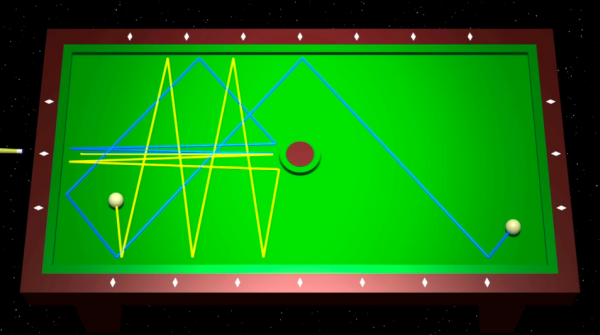
この章では,アダマールの考え方を,これとは違うけれども,最後には逆の曲率を持つ曲面上の測地線とほとんど同じになる例をとって説明している:ビリヤードだ.ビリヤード台の中央に円形の障害物を置いたらどうなるだろうか?ほとんど同じ方向に転がされた2つの玉の軌道は,すぐに全く違ったものになる.

もっと面白いことが起こる.ビリヤード台に3つの円形の障害物A,B,Cを置くと,3つの文字ABCで書かれ,(隣同士が異なる)任意の単語,例えばABABCABCに対し,その順番で円板に当たる周期軌道がただ1つ存在する.この3つの文字A,B,Cで書かれた単語による軌道の符号付けは,実数の記法と同じ種類のものである…
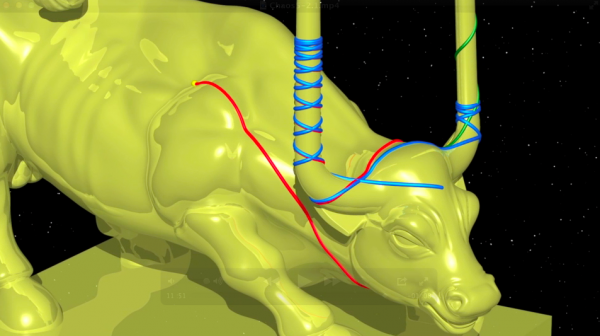
デュエムは雄牛の額の上を滑っていく質点を次のように比喩的に描写している.
« まず,閉じた測地線がある.また,正確に出発点に戻ってくることなく,無限には離れていくこともない測地線もある;これらには,右の角の周りを回り続けるものもあり,左の角の周りを回り続けるものもある,[…]他のもっと複雑なものは,ある規則に従って一方の角の周りを何回か回り,他方の角の周り何回か回るということを繰り返す[…].この雄牛の額の上には[…],無限遠に向かう測地線もあり,右の角を登っていくものもあれば,左の角を登っていくものもある[…].»

ほとんど同じ方向に向かっていった2つの測地線が,デュエムが見事に説明しているように,まったく異なる未来を持っているのである.
«今考えている曲面上で,質点が幾何的に与えられた点を幾何的に与えられた速度で動き始めれば,数学的にこの点の軌道が定まり,この点が無限遠に向かうかどうかが決定される.しかし,物理学者にとっては,この数学的議論は永久に使い物にならない. »
この微妙な差をわかってほしい:数学的結論は得られるが,それは物理学者にとっては使い物にならない.理論と現実のあいだには,大きな隔たりがある.
以下のフランス語版の第5章をご覧ください.他の言語を選ぶ,章のリストを見る,字幕のリストを見る,このビデオを利用するためのライセンスの情報を見る,これらのためには,「このビデオについて」のページをご覧ください.
