O touro de Duhem

Para abordar uma questão tão complexa como a do movimento dos corpos celestes é bem razoável começar o estudo por situações mais simples. Se o movimento de uma bola de bilhar rolando sem atrito dentro de uma cuba não parece muito difícil de compreender, será diferente se a cuba estiver amassada... Sim, o movimento se torna, de repente, muito complicado.

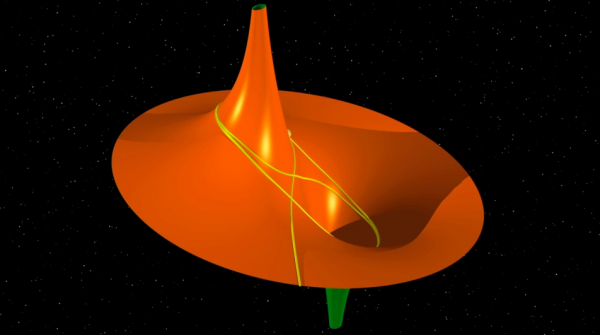
No início do século XX , o filósofo das ciências Pierre Duhem (1861-1916) apresentou, com humor, os trabalhos do matemático Jacques Hadamard (1865-1963), publicados num artigo intitulado ‘Geodésicas em Superfícies de Curvatura Negativa’, de uma forma figurada: tratava-se de lançar uma bola que rolaria, sem atrito, na testa de um touro cujos chifres se alongassem até o infinito. Que ideia maluca!
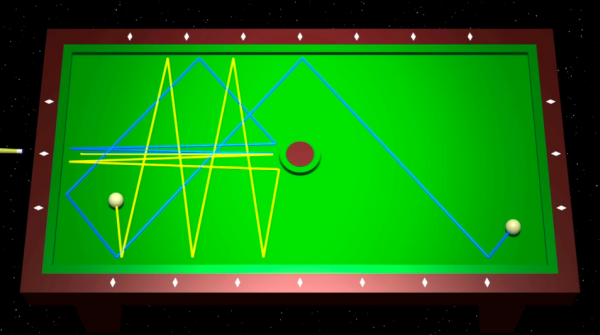
Neste capítulo, tentaremos explicar, as ideias de Hadamard num exemplo diferente mas bem próximo das geodésicas de superfícies de curvaturas negativas : trata-se de um jogo de bilhar. O que aconteceria se colocássemos uma placa circular no meio da mesa de biliar? Duas bolas lançadas em direções muito próximas podem ver suas trajetórias tornarem-se, bem depressa, completamente diferentes.

Mas ainda melhor. Se introduzíssemos três pequenas placas circulares A, B e C sobre a mesa, então para toda palavra formada com as três letras, por exemplo ABABCABC, existe uma única trajetória periódica que toca sucessivamente as três placas na ordem estabelecida pelas letras. Esta codificação de trajetórias descrita com palavras formadas com as letras A, B e C, evoca a escrita dos números reais...
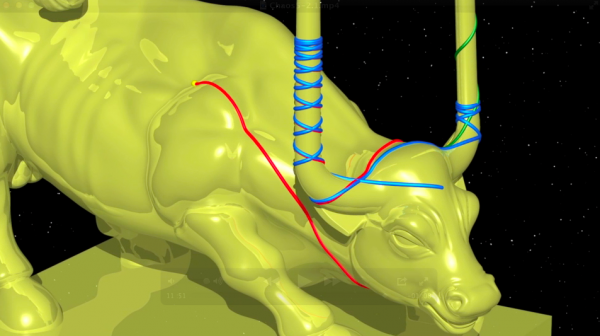
Duhem continua sua descrição imaginada de uma massa material deslizando na testa de um touro de acordo com essas palavras.
« Existem, então, geodésicas que se fecham em si mesmas. E há outras que, sem nunca voltar ao ponto de partida, não se direcionam jamais ao infinito ; algumas percorrem sem cessar em volta do chifre direito, outras, em torno do chifre esquerdo [ ...] e outras, mais complicadas, alternam, segundo certas regras, voltas em torno de um chifre e em torno do outro [...] . Sobre a testa do nosso touro [...] haverá também geodésicas que partem para o infinito, umas gravitando em torno do chifre direito , e outras, em torno do chifre esquerdo [...]. »

Duas geodésicas que partem em direções muito próximas têm futuros diferentes, como explica, muito bem Duhem.
« Se um ponto material for lançado sobre uma superfície conhecida a partir de uma posição geometricamente dada, com uma velocidade geometricamente dada, raciocínios matemáticos podem determinar a trajetória deste ponto e dizer se esta trajetória vai ou não ao infinito. Mas, para o físico, esta dedução é totalmente inútil. »
Observem a sutileza: a dedução matemática é possível mesmo que seja inútil para o físico. Entre a teoria e a prática existe um mundo inteiro.
CAPÍTULO ANTERIOR CAPÍTULO SEGUINTE
Abaixo o capítulo V em português. Para escolher uma outra língua, acessar a lista de todos os capítulos e títulos, ou obter informações sobre a licença sob a qual este filme é difundido, ver a página O filme.
