乐高积木的赛跑

在17世纪末,戈特弗里德·莱布尼茨与艾萨克·牛顿分别独自地发明了一种极其智慧的数学工具:无穷小微积分又名微积分:一个能够预测未来的无比灵验的水晶球,前提是已确知系统的现状以及施加于系统的力;这样的计算我们称作解微分方程。本片的第二章将会用乐高人仔为大家做一个简单的介绍。

我们该如何定义一个乐高人仔走路时的速度?我们知道平均速度是用他经过的距离和他经过这段距离所用的时间的比例来定义的。用这个方法,我们可以计算出他走每步的平均速度。
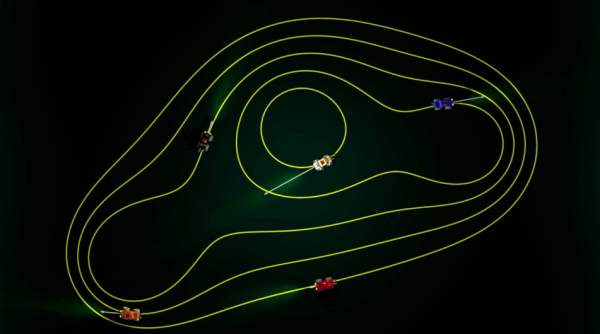
可是对于一辆行驶中的汽车的速度呢?这个问题的关键是我们把它的运动分割为一小段一小段的运动,这些分割后的运动非常的短以至于它们不会被发现。这就是导数或者微分的基础
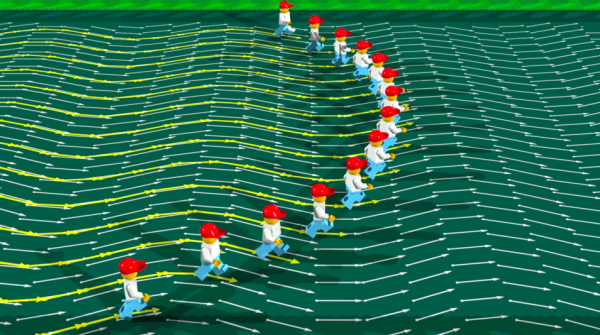
想象一条流动的河流,对于河流的每一点,我们完全有可能去计算水流在那一点的速度。我们然后绘制一段河流,并在问题中的那一点上画一个箭头,箭头的长度表示了速度的大小,箭头的方向表示了速度的方向。我们称这样的箭头为向量。对于河流中的任意一点,我们都可以画出这样一个向量。数学家把这些所有的向量称为向量场。

积分是微分的反面。我们现在的任务是计算一个给定向量场的轨迹。影片将会展示一个乐高人仔在向量场中按照一个给定路径的运动。在数学上,这就是柯西—莱布尼茨
定理,它总结了绝对论:给定一个向量场,给定一个初始状态,那么仅有一条由初始状态出发的轨迹,并且此轨迹处处与速度向量相切。

正如我们已经用一个简单例子证明的,绝对论有其局限性。在1879年,物理学家詹姆斯·克拉克·麦克斯韦(1831-1879)强调了初始状态对于物理现象的重要性。
有句格言说道……相同的原因总会导致相同的结果……另有一句不可混为一谈的格言
:「相近的原因导致相近的后果」,这句格言成真的前提是我们已知初始状况的微小变化仅能导致终极状态的微小变化。对于许多物理现象,这个条件却能成立;不过有些时候,即使是初始的微小变化,也能导致系统的末状态的巨变。

在本章的最后,我们看到了我们的乐高人仔在他们的飞行器中翱翔。这些图像现在可以告诉我们,在三维空间之中,情况会变得相当复杂。
VERSION PDF DE CETTE PAGE ET COMMENTAIRES DU CHAPITRE
CHAPITRE PRÉCÉDENT CHAPITRE SUIVANT
Ci-dessous le chapitre II en français. Pour choisir une autre langue, avoir accès à la liste de tous les chapitres et sous-titres, ou obtenir des informations à propos de la licence sous laquelle est diffusé ce film, voir la page Le film.

